|
A little mathematical understanding is unavoidable in order to manipulate numbers in stoichiometric calculations. One of the concepts encountered is percentage, %. Syllabus referenceStructure 1.4.4 - The empirical formula of a compound gives the simplest ratio of atoms of each element present in that compound. The molecular formula gives the actual number of atoms of each element present in a molecule.
Guidance Tools and links
|
The term "percentage" means parts in every hundred. Simple fractions may be scaled up to be out of one hundred when the numerator (the number on the top) becomes the percentage.
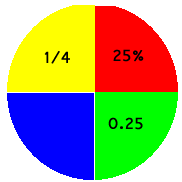
One quarter is written 1/4 or, out of one hundred, this becomes 25/100 = 25%
It is useful to become familiar with the relationship between simple fractions, decimals and percentages.
|
fraction
|
decimal
|
percentage
|
|---|---|---|
|
1/2
|
0.50
|
50%
|
|
1/3
|
0.33
|
33%
|
|
2/3
|
0.67
|
67%
|
|
1/4
|
0.25
|
25%
|
|
3/4
|
0.75
|
75%
|
|
1/5
|
0.20
|
20%
|
|
2/5
|
0.40
|
40%
|
|
3/5
|
0.60
|
60%
|
|
4/5
|
0.80
|
80%
|
|
1/8
|
0.125
|
12.5%
|
The percentage composition of a material is generally taken to mean the percentage by mass of the elements within a substance.
|
Example: Calcium carbonate - CaCO3 The relative formula mass = 40 + 12 + (3x16) = 100 Calcium makes up 40 relative mass unit parts of this formula, therefore the percentage by mass of calcium is 40/100 = 40% Carbon makes up 12 relative mass unit parts of this formula, therefore the percentage by mass of carbon is 12/100 = 12% Oxygen makes up 48 relative mass unit parts of this formula, therefore the percentage by mass of oxygen is 48/100 = 48% |
The empirical formula is the simplest ratio of atoms within a chemical compound.
From the above example it may be appreciated that the percentage by mass, when divided by the relative mass of each element, gives the relative numbers of particles in the formula.
|
Example: Find the empirical formula of the compound which has the following percentage by mass composition: Carbon 12.12%; Oxygen 16.16%; Chlorine 71.17%. Divide each percentage composition by mass by the relative atomic mass. Carbon 12.12/12 = 1.01, Oxygen 16.16/16 = 1.01, Chlorine 71.17/35.5 = 2.00 These are in the approximate integer ratio 1xC : 1xO : 2xCl Thus the empirical formula = COCl2 |
This method is used to calculate the empirical formula of unknown substances. If we also know the relative formula mass, obtainable from experimental data, then the molecular formula can also be found.
Why bother with the empirical formula?
It may seem at first sight that an unusual emphasis is placed on this procedure by the various examination boards. This stems from the historic development of chemistry, from the times when determination of structure was an extremely important activity, as many new materials were being isolated and their formulae determined.
An unknown compound would be broken down into simpler substances and these measured quantitatively. By finding the percentage of the elements within the original compound it became possible to determine the empirical and, with further evidence, the molecular formula of the unknown compound.
|
Example: 1.6 g of an unknown organic substance X was burned in excess oxygen and the mass of carbon dioxide produced determined by absorption in concentrated KOH solution. The mass of water was determined by first passing the gases produced from the combusion through anhydrous calcium choride. The following results were obtained:
Mass of carbon in 4.889g CO2 = 4.889 x 12/44 = 1.333g Mass of hydrogen in 2.405g of H2O = 2.405 x 2/18 = 0.267g percentage by mass of carbon = 1.333/1.6 = 0.833 x 100 = 83.3% percentage by mass of hydrogen = 0.267/1.6 = 0.167 x 100 = 16.7% empirical formula = carbon 83.3/12 : hydrogen 16.7/1 empirical formula = C 6.94 : H 16.7 This simplifies to give an empirical formula of C5H12 |
In summary, it is important to be able to calculate the percentage composition by mass of the elements within a compound and also to use percentage composition values to calculate the empirical formula. Remember that the sum of all of the percentages by mass MUST equal 100%.

