|
Acidity is generally used in the Arrhenius definition, with measurements being taken in aqueous solution. The water solvent is very much implicated in the dissociation process of the acids and bases, solvating the ions that are formed. Syllabus referenceReactivity 3.1.5 - The ion product constant of water, Kw, shows an inverse relationship between [H+] and [OH-]. Kw = [H+][OH-]
Guidance
Tools and links
|
The dissociation of water
Water partially dissociates into ions according to the equation:
| H2O |
This dissociation can be expressed according to the equilibrium law:
.gif) |
However, the concentration of water is in huge excess and effectively remains constant (to a very close approximation), as only a tiny fraction of the molecules break apart. The [H2O] term can be removed and a new constant, Kw, defined.
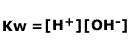 |
The constant Kw, sometimes called the ionic product of water remains unchanged at constant temperature (as all good constants should!).
| Kw = 1 x 10-14 mol2 dm-6 (25ºC) |
From the stoichiometry of the equation, the concentration of hydrogen ions equals the concentration of hydroxide ions. Therefore the concentration of hydrogen ions in pure water at 25ºC = the square root of the ionic product of water:
| = 1 x 10-7 mol dm-3 |
The constant Kw is only affected by temperature. It can be used to find the hydrogen ions concentration from the hydroxide ion concentration and vice versa.
|
Example: Find the hydrogen ion concentration in a solution of 0.01 mol dm-3 sodium hydroxide solution. Sodium hydroxide is a strong base and dissociates 100% in solution.
Therefore the [OH-] = 0.01 mol dm-3 [OH-] x [H+] = 1 x 10-14 mol2 dm-6 Therefore [H+] = 1 x 10-14 /0.01 = 1 x 10-12 mol dm-3 |
|
Example: What is the concentration of OH- ions (in mol dm-3) in an aqueous solution in which [H+] is 2.0 x 10-3 mol dm-3? (Kw = 1.0 x 10-14 mol2 dm-6) . We know that [H+][OH-] = Kw = 1.0 x 10-14 mol2 dm-6 Therefore [OH-] = 1.0 x 10-14 / [H+] Therefore [OH-] = 5.0 x 10-10 mol dm-3 |
Variation of Kw with temperature
All equilibrium constants are temperature dependent (and this one is no exception):
The dissociation of water molecules into ions is an endothermic process (energy must be absorbed to break the bonds). Endothermic processes are favoured by an increase in temperature, hence as the temperature increases the equilibrium moves further to the right hand side and Kw gets larger.
As Kw gets larger so do the values of the hydrogen ion concentration and the hydroxide ion concentration.
pH is a measure of the hydrogen ion concentration (pH = -log[H+]), as the temperature increases the pH gets lower.
| H2O |
Consequently, according to Le Chatelier, an increase in temperature favours the forward reaction - i.e. the position of equilibrium shifts towards the right hand side and Kw becomes larger.
However, as the ratio of hydrogen ions to hydroxide ions in pure water must remain 1:1, then if we know the value of Kw, it is a simple matter to calculate the value of either H+ or/and OH- to obtain the concentrations and hence the values of pH and pOH.
|
Example:Calculate the pH when Kw = 6.5 x 10-14 mol2 dm-6
and...
Then...
Therefore...
The pOH value is the same, as [H+] =[OH-] |

