Higher-level only
Ionic substances exist in giant structures of repeating ions all held together by electrostatic forces.
Syllabus ref: R1.2.5Reactivity 1.2.5 - A Born–Haber cycle is an application of Hess’s law, used to show energy changes in the formation of an ionic compound. (HL)
- Interpret and determine values from a Born–Haber cycle for compounds composed of univalent and divalent ions.
Guidance
- The cycle includes: ionization energies, enthalpy of atomization (using sublimation and/or bond enthalpies), electron affinities, lattice enthalpy, enthalpy of formation.
- The construction of a complete Born–Haber cycle will not be assessed.
Tools and links
- Structure 2.1 - What are the factors that influence the strength of lattice enthalpy in an ionic compound?
Electrostatic force between ions
Although not a bond in the classical covalent sense of the word, electrostatic forces hold oppositely charges ions together in an ionic crystal lattice. This force is dependent on the magnitude of the charges on the ions and inversely proportional to the distance between them.
![]()
Where: z1 is the magnitude of the positive ion, z2 is the magnitude of the charge on the negative ion and 'r' is the distance between them.
Consequently, ions with greater charges are held together more tightly and smaller ions form more effective bonds than larger ions. The following examples should make the effect of changing both ionic charge and ionic radius clear.
|
Example: The force of attraction between sodium and chloride ions: This is dependent on the magnitude of the ionic charges. Sodium ions
have a 1+ charge and chloride ions have a 1- charge.
Therefore the distance between is 0.098 + 0.181 = 0.279nm The force of attraction is proportional to 1 x 1 /(0.279)2 = 12.8 This number is meaningless in isolation, but could be used to compare the force of attraction between other ions in an ionic lattice. You will not be asked to do this in an exam |
The previous example considered the force between two singly charged ions. For comparison we can look at the force of electrostatic attraction between two singly charged ions of different radii, such as caesium iodide.
|
Example: The force of attraction between caesium and iodide ions: This is dependent on the magnitude of the ionic charges. Caesium ions have a 1+ charge and iodide ions have a 1- charge. The distance between them is the sum of the ionic radii of the two ions.
Therefore the distance between is 0.169 + 0.219 = 0.388nm The force of attraction is proportional to 1 x 1 /(0.388)2 = 6.6 We can see that this value, proportional to the electrostatic force of attraction, is about one half that of sodium chloride. The 'bond' is weaker. |
A similar comparison could examine the effect of changing the magnitude of charge on the ions, for example in the force of attraction between magnesium and oxide ions in magnesium oxide.
|
Example: The force of attraction between magnesium and oxide ions: Magnesium ions have a 2+ charge and oxide ions have a 2- charge. The distance between them is the sum of the ionic radii of the two ions.
Therefore the distance between is 0.065 + 0.140 = 0.205nm Thus, the force of attraction is proportional to 2 x 2 /(0.205)2 = 95.2 This value is far bigger than that of sodium chloride, a factor of seven times. The force of attraction between magnesium and oxide ions is considerably larger than that of sodium chloride. |
Forces within the lattice
An ionic lattice is the giant framework of repeating positive and negative ions in three dimensions. In the section above we looked at the forces that exist between two oppositely charged ions.
In an ionic lattice each positive ion is surrounded by negative ions and so feels a force of attraction towards all of them. The same case applied to each negative ion, it is surrounded by positive ions and feels the forces of attraction towards all of these neighbours.
Sodium ion surrounded by chloride ions
Chloride ion surrounded by sodium ions
The whole crystal lattice consists of billions upon billions of these ions, each positive surrounded by negative ions and each negative surrounded by positive ions. The forces of attraction pull all of the ions into the best arrangement possible in which all of the forces are at a maximum. This gives us the final crystal lattice structure:
The lattice enthalpy
The electrostatic forces hold the crystal lattice together. To break the lattice apart and overcome these forces, energy must be applied. The amount of energy required to break apart one mole of an ionic lattice is called the lattice enthalpy.
Definition
Lattice enthalpy is the energy required to break 1 mole of an ionic lattice into its individual constituent ions at infinite separation. It is an endothermic process, ΔH is +ve.
NaCl(s) → Na+(g) + Cl-(g)
Note that some examination boards define lattice enthalpy as the energy released on forming one mole of a crystal lattice from its constituent gaseous ions at infinite separation. Numerically, of course, this has the same magnitude but different sign.
By considering the number of nearest neighbours, the structural arrangement of the ions and the types of ions involved in a lattice, it is possible to calculate the total sum of the forces involved in a specific lattice and from this, the energy required to break up the lattice into individual ions in a gaseous state.
This is called the theoretical lattice enthalpy.
Lattice enthalpies are usually found experimentally , the experimental lattice enthalpy. If there is good agreement between the theoretical and the experimental values, the crystal structure is considered to be totally ionic.
Poor agreement suggests that the structure is not entirely ionic.
Hess' law
Hess' law is the fundamental basis behind the calculation of all thermodynamic quantities. The principle can be applied to ionic systems by considering the different energy changes required to get from one situation to another.
When Hess' law is applied to the standard enthalpy of formation of an ionic lattice, the different stages form a cycle, called a Born-Haber Cycle.
Born-Haber Cycles
The enthalpy of formation of a compound is defined as the energy change when 1 mole of a compound is formed from its constituent elements in their states under standard conditions.
For an ionic compound it is the formation of 1 mole of an ionic lattice from its constituent elements in their standard states:
Na(s) + ½Cl2(g) → NaCl(s)
Notice the difference between the equation above and that of the lattice enthalpy, which forms the lattice from gaseous ions.
The Born Haber cycle must begin with the elements in their standard states and arrive finally at the ions in position within 1 mole of a lattice. For this, several theoretical energy transformations must take place. These processes are best considered while referring to a specific example, in this case sodium chloride.
1 - The metal (sodium) must be turned into separate gaseous atoms - atomisation. This is an endothermic process as energy is required to overcome the metallic bonding forces. This is can also be referred to as vaporisation for elements that form atomic vapours (such as a metal)
Na(s) → Na(g)
2 - The non-metal must be turned into separate gaseous atoms - in the case of chlorine this means breaking half a mole of bonds to give one mole of atoms. It is one half the bond enthalpy of chlorine. This can also be referred to as atomisation. However, it is important to note the difference between the definitions of atomisation enthalpy (energy quoted per mole of atoms formed) and the bond dissociation enthalpy (energy quoted per mole of bonds broken = 2 moles of atoms formed).
½Cl2(g) → Cl(g)
3 - The gaseous metal atoms must be ionised to form gaseous ions - this is the first ionisation energy of sodium. For atoms that have double charges there are two ionisations involved, the first ionisation energy and the second ionisation energy. You may be given the two values separately, or combined together.
Na(g) → Na+(g)
4 - The chlorine atoms must be turned into ions. For a non-metal this involves adding an electron to the atom. This is an exothermic process called the electron affinity of chlorine. For negative ions with a double charge there are two electron affinities involved, the first electron affinity and the second electron affinity. The energies may be give to you separately, or combined into one value.
Cl(g) → Cl-(g)
5 - The gaseous ions can then be brought together into the lattice. This is the opposite of the lattice enthalpy and is exothermic. Remember that the lattice enthalpy is defined by the IBO as the energy required to break the lattice. In the Born Haber cycle the step is usually shown as forming the lattice. This should not be a problem providing you understand that breaking the lattice must be an endothermic process.
Na+(g) + Cl-(g) → NaCl(s)
Hess' law tells us that the sum of the energies of all of these steps must equal the enthalpy of formation, as it also takes us from the same starting point to the same conclusion. Born-Haber presents this idea in a graphical form, with the endothermic steps on the left and the exothermic steps on the right.
To use a Born-Haber cycle your starting point and your destination are given by the question's requirements. You simply add up all of the quantities along the alternative route, taking into account whether the energy change is negative or positive in the direction you are going.
Note: Construction of Born-Haber cycles will not be examined in the IB Chemistry 2025 syllabus
Doubly charged ions
In compounds that involve doubly charged ions, such as magnesium or oxide, there are a couple more steps to take into account in the Born-Haber cycle.
The ionisation step of the metal atom, for example magnesium, must be performed twice to arrive at a double plus ion:
Mg(g) → Mg+(g) + 1e
Mg+(g) → Mg2+(g) + 1e
These are the first ionisation energy and the second ionisation energy of magnesium. They are both endothermic processes.
For the non-metal ion, eg oxide, there are two electron affinity steps to arrive at the double negative ion.
O(g) + 1e → O-(g)
O-(g) + 1e → O2-(g)
The first of these steps is exothermic, but the second electron affinity is always endothermic, as an electron is being added onto an already negatively charged species. This means that the Born-Haber cycle steps back upwards on the diagram. In terms of the calculations it makes no difference, as the values of the two electron affinity steps are simply included with the correct signs into the calculation. An alternative, easier, approach is to add the two electron affinities together before including them in the cycle.
Example: Born Haber cycle for magnesium oxide:
Although the cycle looks confusing it is just the same as that of sodium chloride with two extra steps (one extra ionisation energy and one extra electron affinity) added in. These extra steps could be combined with their corresponding similar steps (eg first and second ionisation energies combined) before constructing the cycle, providing you make it very clear that you have done this.
Calculations
The actual calculations using a Born-Haber cycle are very simple. The only complication arises when the signs of the enthalpy change need to be reversed, or when the quantities of each component are not equivalent to the enthalpy change in question. We will deal with these complications as they arise.
As the enthalpy of formation equals the sum of all of the oter steps, then if we are missing only 1 piece of data we can always work it out using the Born-Haber cycle. For example, in the case of sodium bromide, if we do not know the electron affinity of bromine, but all of the other quantities are known, then rearranging the equation:
ΔHf(NaBr) = ΔH(atomisation Na) + ΔH(1st ionisation Na) + ½ΔH(bond dissociation Br2) + ΔH(electron affinity Br) - ΔH(lattice enthalpy NaBr)
Gives:
ΔH(electron affinity Br) = ΔHf(NaBr) + ΔH(lattice enthalpy NaBr) - ΔH(atomisation Na) - ΔH(1st ionisation Na) - ½ΔH(bond dissociation Br2)
* Note that the lattice enthalpy sign is reversed in the original equation, i.e. it is given a negative sign, as we are really dealing with the reverse of the lattice enthalpy, the energy released when the lattice is formed.
|
Example: Given the following information, calculate the lattice enthalpy of the sodium chloride lattice:
From the Born-Haber cycle, the enthalpy of formation equals the sum of all of the other steps involved. However, the bond dissociation enthalpy provides 2 moles of chlorine atoms and we only require 1 mole. Thus we use one half of this value. ΔHf(NaCl) = ΔH(at. Na) + ΔH(1st i.e. Na) + ½ΔH(b.d. Cl2) + ΔH(1st e.a. Cl) + (-)ΔH(lattice NaCl) Note that we are using the reverse of the lattice enthalpy, as we are forming the lattice from its ions. Substitute the values: -411 = 107 + 496 + ½(242) + -349 + (-)ΔH(lattice NaCl) Rearrange: ΔH(lattice NaCl) = 411 + 107 + 496 + 121 - 349 = 786 kJmol-1 |
Worked examples
Q452-01 For which of the following is ΔH- O+(g) + e- → O(g)
- O(g) + e → O-(g)
- O-(g) + e → O2-(g)
- O(g) + O(g) → O2(g)
|
The second electron affinity of oxygen is positive as two negative charges are being forced together. Response C |
Q452-02 The first ionization energy for a mole of magnesium atoms is the energy required for which of the following processes?
- Mg(s) → Mg(g)
- Mg(g) → Mg+(g) + 2e
- Mg+(g) → Mg2+(g) + e
- Mg(g) → Mg+(g) + e
|
The single charged ions ions are formed from 1 mole of gaseous atoms. Response D |
Q452-03 The formation of an ionic compound from its elements can be understood in terms of steps, each involving a certain energy input or output. Which energy step usually dominates all others in the formation of a stable ionic compound?
- ionization energy
- electron affinity
- lattice energy
- dissociation energy
|
The lattice energy is usually by far the greatest in magnitude. Response C |
Q452-04 The following enthalpy changes (in kJ mol-1) refer to sodium chloride and its constituent elements:
| ΔHº formation of sodium chloride | -411 kJ |
| ΔHº atomisation sodium | +109 kJ |
| ΔHº atomisation chlorine | +121 kJ |
| 1st ionisation energy sodium | +494 kJ |
| 1st electron affinity chlorine | -364 kJ |
a) State the meaning of the + and - signs in the enthalpy values [1]
Explain the meaning of the symbol 'º'. [1]
b) The given values can be used to calculate the lattice enthalpy of sodium
chloride.
Define the term 'lattice enthalpy' [1]
Construct a Born-Haber cycle and hence calculate the lattice enthalpy of sodium
chloride [4]
|
a) the signs show whether the process is exothermic (negative) or endothermic (positive). The 'º' symbol indicates that all of the values are measured
under standard conditions of 298K, 1 atmosphere pressure. b) The lattice enthalpy is the energy required to separate 1 mole of a crystalline lattice into its individual gaseous ions at infinite separation (by this definition, it is always positive) 1 is the enthalpy of formation of NaCl = -411 kJ 2 is the enthalpy of atomisation of sodium = +109 kJ 3 is the enthalpy of ionisation of sodium = +494 kJ 4 is the enthalpy of atomisation of chlorine = +121 kJ 5 is the electron affinity of chlorine = -364 kJ 6 is the reverse (negative) of the lattice enthalpy 6 = -1 + 2 + 3 + 4 + 5 Thus the lattice enthalpy = (411 + 109 + 494 + 121 -364) = 771 kJ |
Q452-05 Using the following thermodynamic data, calculate the lattice enthalpy of lithium oxide:
| Li(g) → Li+(g) + e | +540 kJ |
| Li(s) → Li(g) | +146 kJ |
| O2(s) → 2O(g) | +488 kJ |
| O(g) + 2e → O2-(g) | +598 kJ |
| 2Li(s) + ½O2(g) → Li2O(s) | -586 kJ |
|
1 is the enthalpy of formation of Li2O = -586 kJ 2 is 2 x the enthalpy of atomisation of lithium = 2 x (+146) = 292 kJ 3 is 2 x the enthalpy of ionisation of lithium = 2 x (+540) = 1080 kJ 4 is 1/2 the bond dissociation enthlapy of oxygen = 1/2 x (+488) = 244 kJ 5 is the sum of first and second electron affinities of oxygen = +598 kJ 6 is the reverse (negative) of the lattice enthalpy 6 = -1 + 2 + 3 + 4 + 5 Lattice enthalpy = 586 + 292 + 1080 + 244 + 598 = 2800 kJ |
Q452-06 Use the following thermodynamic data to calculate the lattice enthalpy of barium iodide:
| Ba(g) → Ba2+(g) + 2e | +1440 kJ |
| Ba(s) → Ba(g) | +142 kJ |
| I2(g) → 2I(g) | +144 kJ |
| I(g) + e → I-(g) | -288 kJ |
| Ba(s) + I2(s) → BaI2(s) | -608 kJ |
| I2(s) → I2(g) | + 38 kJ |
Answer
|
1 is the enthalpy of formation of BaI2 = -608 kJ 2 is the enthalpy of vaporisation of iodine = 38 kJ 3 is the enthalpy of atomisation of barium = 142 kJ 4 is the sum of first and second ionisation energies of barium = +1440 kJ 5 is bond dissociation enthalpy of iodine = +144 kJ 6 is 2 x the electron affinity of iodine = 2 x (-288) = -576 kJ 7 is the reverse of the lattice enthalpy. 7 = -1 + 2 + 3 + 4 + 5 + 6 Lattice enthalpy = 608 + 38 + 142 + 1440 + 144 - 576 = 1796 kJ |
Q452-07 Use the following thermodynamic data to calculate the enthalpy of atomisation of zinc:
| Zn(g) → Zn2+(g) + 2e | +2680 kJ |
| Zn2+(g) + O2-(g) → ZnO(s) | -3980 kJ |
| O2(g) → 2O(g) | +488 kJ |
| O(g) + 2e → O2-(g) | +598 kJ |
| Zn(s) + ½O2(s) → ZnO(s) | -342 kJ |
Answer
|
We must choose the alternative route to get from Zn(s) to Zn(g). This involves passing anticlockwise around the cycle. 2 = 1 + 6 - 5 - 4 - 3 Atomisation enthalpy of zinc = -342 - (-3980) - 598 - ½(488) - 2680 Atomisation enthalpy of zinc = 116 kJ |
Q452-08 Use the following thermodynamic data to calculate the sum of the first two ionisation energies of calcium:
| O2(g) → 2O(g) | +488 kJ |
| Ca(s) → Ca(g) | +158 kJ |
| O(g) + 2e → O2-(g) | +598 kJ |
| Ca2+(g) + O2-(g) → CaO(s) | -3328 kJ |
| Ca(s) + ½O2(s) → CaO(s) | -628 kJ |
Answer
|
Ca(g) → Ca2+(g) This is step 3 on the Born-Haber cycle. We must choose the alternative route to get from Ca(g) to Ca2+(g). This involves passing anticlockwise around the cycle from Ca(g) to Ca2+(g). 3 = -2 + 1 - 6 - 5 - 4 Sum of the first two ionisation enthalpies of calcium = -158 + (-628) - (-3328) - 598 + ½(-488) Sum of the first two ionisation enthalpies of calcium = 1700 kJ |
Q452-09 Use the following thermodynamic data to calculate the bond dissociation enthalpy of fluorine:
| Na(g) → Na+(g) + e | +486 kJ |
| Na(s) → Na(g) | +98 kJ |
| Na+(g) + F-(g) → NaF(s) | -906 kJ |
| F(g) + e → F-(g) | -318 kJ |
| Na(s) + ½F2(g) → NaF(s) | -564 kJ |
|
F2(g) → 2F(g) Notice that this is twice energy change 4 in the Born-Haber cycle. Step 4 = -3 - 2 + 1 - 6 - 5 Thus ½ x ΔH(bde) of fluorine = -486 - 98 + (-564) -(-906) -(-318) = 76 ∴ the ΔH(bde) of fluorine = 152 kJ |
Q452-10 Use the following thermodynamic data to calculate the enthalpy of atomisation of manganese:
| Mn(g) → Mn2+(g) + 2e | +2230 kJ |
| Br2(l) → Br2(g) | +18 kJ |
| Br2(g) → 2Br(g) | +186 kJ |
| Br(g) + e → Br-(g) | -322 kJ |
| Mn2+(g) + 2Br-(g) → MnBr2(s) | -2386 kJ |
| Mn(s) + Br2(l) → MnBr2(s) | -372 kJ |
Answer
|
Mn(s) → Mn(g) Notice that this energy change 3 in the Born-Haber cycle. Step 3 = -2 + 1 +7 -(2 x 6) - 5 - 4 Thus ΔH(at) of manganese = -18 + (-372) + 2386 - 2(-322) - 186 - 2230 = +224 ∴ the ΔH(at) of manganese = +224 kJ |
Q451-11 The lattice enthalpies for sodium chloride, potassium chloride and potassium bromide are + 780, +710 and +680 kJ mol-1 respectively. Comment on these results and suggest a value for that of lithium chloride.
Answer
|
Comparing NaCl and KCl, we see that the lattice enthalpy of NaCl is larger. This is due to the smaller radius of the sodium ion compared to the potassium ion. Comparison of KCl and KBr, we see that KCl has a larger lattice enthalpy than KBr, once again due to the smaller radius of the chloride, as compared to the bromide ion. Lithium is a much smaller ion than sodium, so the lattice enthalpy of lithium chloride would be expected to be greater than that of sodium chloride. In fact it is +846 kJ. |
Q451-12 In which of the following are the compounds CaF2, CaCl2, CsF, and LiF arranged in order of increasing lattice enthalpy?
- CaCl2, CaF2, CsF, LiF
- CsF, LiF, CaCl2, CaF2,
- CaCl2, CaF2, LiF, CsF
- CaCl2, CaF2, CsF, LiF
- LiF, CaF2, CsF, CaCl2
|
Larger lattice enthapy is caused by greater magnitude of ionic charge and smaller radius. The ionic charge is the most important of the two. The correct order is CsF < LiF (smaller ion has a larger lattice enthalpy) and then CaCl2 < CaF2, these both have a double plus calcium ion and so greater lattice enthalpies than the first two. The fluoride ions are smaller than chloride ions and so cause greater lattice enthalpy in CaF2. |
Q451-13 Which combination of ionic charge and ionic radius give the largest lattice enthalpy for an ionic compound?
|
Ionic charge
|
Ionic radius
|
|
| A. |
high
|
large
|
| B. |
high
|
small
|
| C. |
low
|
small
|
| D. |
low
|
large
|
|
Lattice enthalpy increases with decreasing ionic radius and increasing magnitude of charge. Response B |
Q451-14 The lattice enthalpy values for lithium fluoride and calcium fluoride are shown below:
- LiF(s) ΔH = +1022 kJ mol-1
- CaF2(s) ΔH = +2602 kJ mol-1
Which of the following statement(s) helps to explain why the value for lithium fluoride is less than that of calcium fluoride?
- 1. The ionic radius of lithium is less than that of calcium
- 2. The ionic charge of lithium is less than that of calcium
- 1 only
- 2 only
- 1 and 2 only
- Neither 1 nor 2
|
Both lithium fluoride and calcium fluoride have the fluoride ion in common, therefore we can discount this as having an influence on the different values. Calcium ions have a double positive charge, whereas lithium ions have a single positive charge. This creates a much larger force in calcium fluoride than in lithium fluoride. It is a contributory factor. The smaller ionic radius of lithium ions, as compared to calcium ions, would produce a stronger force in the lithium fluoride lattice. This does not contribute to the greater lattice enthalpy of calcium fluoride. Response B |
Q451-15 Which of the following reactions has the most negative ΔH
- LiF(s) → Li+(g) + F-(g)
- Li+(g) + F-(g) → LiF(s)
- NaCl(s) → Na+(g) + Cl-(g)
- Na+(g) + Cl-(g) → NaCl(s)
|
Formation of bonds is exothermic, ruling out A and C. The ions are smaller in B, therefore the lattice formation is more exothermic. Response B |
Q451-16 The lattice enthalpy of CaCl2(s) is -2260 kJ/mol and the enthalpy of hydration is –2340 kJ/mol. How much heat will be released when 0.25 mol of CaCl2(s) dissolves in water?
Answer
|
Energetically, the process of dissolution involves a crystal lattice first breaking apart and then the individual ions are hydrated. The first step is the lattice enthalpy in the endothermic direction (lattice breaking):
The sum of the hydration of the ions:
Dissolution involves both of these steps = +2260 - 2340 = -80 kJ mol-1 The question asks for the energy change when 0.25 moles of calcium chloride are dissolved. Energy change on dissolution of 0.25 moles = 0.25 x -80 = -20 kJ |
Q451-17 Which equation represents the lattice enthalpy of magnesium oxide?
- Mg(s) + ½O2(g) → MgO(s)
- Mg2+(g) + O2-(g) → MgO(g)
- Mg2+(g) + ½O2(g) → MgO(s)
- Mg2+(g) + O2-(g) → MgO(s)
|
Lattice enthalpy is the energy required to separate 1 mole of an ionic lattice into gaseous ions at infinite separation. Alternatively, it may be defined as the energy released when 1 mole of a crystal lattice is formed from its constituent ions at infinite separation. Response B |
Q451-18 Which of the following reactions is the most exothermic?
- Li+(g) + F-(g) → LiF(s)
- Na+(g) + Cl-(g) → NaCl(s)
- Mg2+(g) + O2-(g) → MgO(s)
- Ca2+(g) + S2-(g) → CaS(s)
|
For the most exothermic process we are looking for the strongest lattice. Smallest ions with greatest magnitude of charge (more important). C and D both involve doubly charged ions. Of these two choices, magnesium is smaller than calcium AND oxide ions are smaller than sulfide ions. Response C |
Q451-19 Which compound has the highest lattice enthalpy?
- CaO
- CaS
- LiF
- LiI
|
Compounds A and B have double charged ions. Oxide is smaller than sulfide. Response A |
Q451-20 What is a correct equation to represent the lattice enthalpy of magnesium sulfide?
- MgS(s) → Mg(s) + S(s)
- MgS(s) → Mg(g) + S(g)
- MgS(s) → Mg+(g) + S-(g)
- MgS(s) → Mg2+(g) + S2-(g)
|
Lattice enthalpy can be defined as the enthalpy change when 1 mole of a crystal lattice is formed from its constituent ions at infinite separation. Alternatively it may be defined as the enthalpy change when 1 mole of a crystal lattice is separated into individual gaseous ions at infinite separation. In this case it is the latter definition. Magnesium sulfide is separated into gaseous magnesium (2+) and sulfide (2-) ions. Response D |
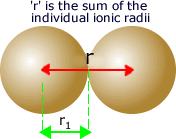 The
distance between them is considered to be the sum of the ionic radii
of the two ions.
The
distance between them is considered to be the sum of the ionic radii
of the two ions. 
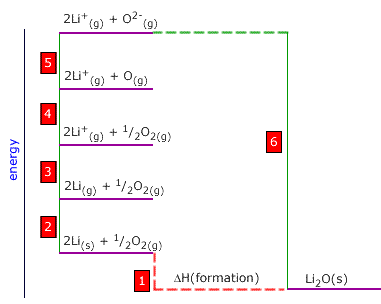 Step
6 is the reverse of the lattice enthalpy. Using the cycle to the right
we can see that the sum of all of the other steps is equal numerically
to the lattice enthalpy.
Step
6 is the reverse of the lattice enthalpy. Using the cycle to the right
we can see that the sum of all of the other steps is equal numerically
to the lattice enthalpy.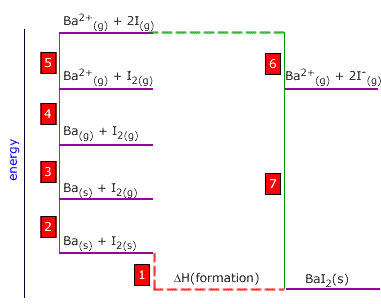 Notice
that here you are given an extra energy step, the formation of gaseous
iodine from solid iodine. This is put into the Born Haber cycle in
the same way as the other enthalpy changes.
Notice
that here you are given an extra energy step, the formation of gaseous
iodine from solid iodine. This is put into the Born Haber cycle in
the same way as the other enthalpy changes.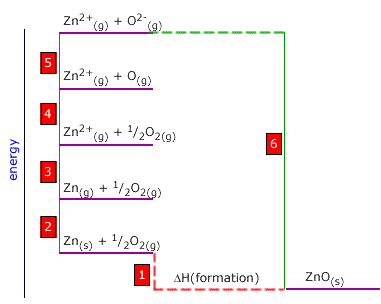 We
are asked to calculate the enthalpy of atomisation of zinc. This is
step 2 on the Born-Haber cycle.
We
are asked to calculate the enthalpy of atomisation of zinc. This is
step 2 on the Born-Haber cycle. 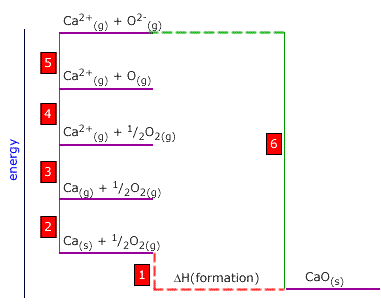 We
are asked to calculate the enthalpy for the process:
We
are asked to calculate the enthalpy for the process: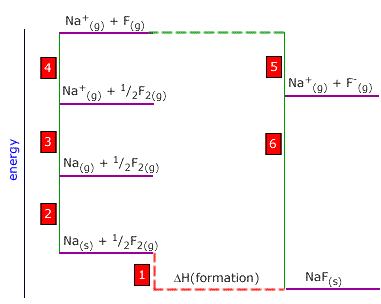 The bond dissociation enthalpy of fluorine is the energy of the following:
The bond dissociation enthalpy of fluorine is the energy of the following: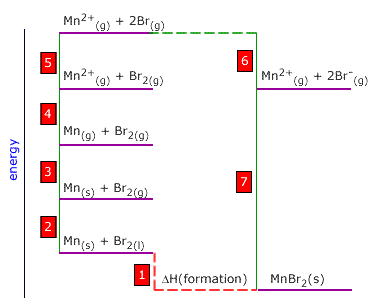 The
atomisation enthalpy of manganese is the energy of the following:
The
atomisation enthalpy of manganese is the energy of the following: