Standard level
It is important to define the term 'reaction rate' before proceding to measure and process data.
Syllabus ref: R2.2.1Reactivity 2.2.1 - The rate of reaction is expressed as the change in concentration of a particular reactant/product per unit time.
- Determine rates of reaction.
Guidance
- Calculation of reaction rates from tangents of graphs of concentration, volume or mass against time should be covered.
Tools and links
- Tool 1, 3, Inquiry 2 - Concentration changes in reactions are not usually measured directly. What methods are used to provide data to determine the rate of reactions?
- Tool 1 - What experiments measuring reaction rates might use time as i) a dependent variable ii) an independent variable?
Definition of rate
As a chemical reaction proceeds the reactants get used up and the products are formed. At any specific time in the course of the reaction the amount (mass, moles, concentration etc) of the reactants compared to the amount at the beginning of the reaction gives us a measure of how far the reaction has gone.
In the same way as a car's velocity is measured in distance travelled/ time taken so the rate of a chemical reaction is measured as change in reactant (or product) amount / time taken
We are usually concerned with the concentration of the reactants and if we can measure how this changes with time then this provides us with the best definition of reaction rate.
Stoichiometry
The stoichiometry (balanced coefficients) of a reaction gives no indication as to the rate of that reaction. It does, however, tell us the relative rate of consumption of reactants and formation of products.
If we examine the reaction between sulfur dioxide and oxygen to form sulfur trioxide in the contact process:
2SO2(g) + O2(g) → 2SO3(g)
On purely stoichiometric grounds, we can see that for every 2 moles of sulfur dioxide that gets used up only 1 mole of oxygen will be consumed. Thus, if the rate of removal of sulfur dioxide is 2 moles per minute, then the rate of removal of oxygen must be 1 mole per minute.
We can, of course, extend this to include the products. If the rate of removal of sulfur dioxide is 2 moles per minute, then the rate of formation of sulfur trioxide is also 2 moles per minute.
Example: Calculate the rate of formation of ammonia in the Haber process, if the rate of consumption of nitrogen is 2 mol s-1.
N2(g) + 3H2(g) → 2NH3(g)
From the equation we can see that the ratio of moles of nitrogen to ammonia is 1:2. Therefore as 1 mole of nitrogen is used up 2 moles of ammonia is formed.
Hence the rate of formation of ammonia = 2 x the rate of consumption of nitrogen.
Therefore the rate of formation of ammonia = 2 x 2 = 4 mol s-1
Reactant concentration
To obtain the rate of change of concentration, we need to know the volume in which the reaction is proceeding. This can be applied to gases as well as solutions. Remember, however, that solids can not be included in calculations of this kind. The concentration of a reactant is usually measured in moles per litre (mol dm-3).
Example: Calculate the concentration of sulfur IV oxide gas if 4 moles occupy 2 litres
Concentration is measured in moles per litre - mol dm-3
Therefore the concentration = 4/2 = 2 mol dm-3
Rate of change of concentration
Combining the above two ideas allows us to calculate rates in terms of concentration change with time. If the concentration changes from 6.2 x 10-3 mol dm-3 to 2.8 x 10-3 mol dm-3 in 20 seconds then the average rate over this portion of the reaction is:
|
Average rate =
|
(6.2 x 10-3) - (2.8 x 10-3)
mol dm-3
|
|
20
|
Average rate = 3.4 x 10-3 mol dm-3 s-1
During the course of a reaction the concentration of reactants decrease as they are used up and at the same time the concentration of the products increases
 |
 |
|
|
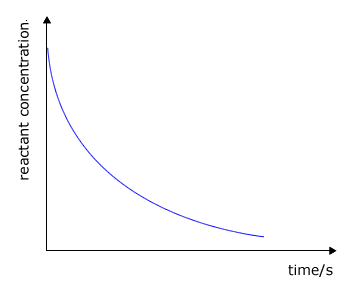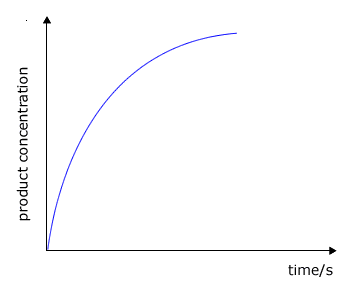reactant concentration against time
|
product concentration against time
|
Initial rate
The rate of change of concentration may be obtained from the graphs above by measuring the gradient of the tangent to the curve. However, it should be apparent that the rate changes as the reaction proceeds. At the start of the reaction the gradient or slope of the curve is at a maximum and gradually decreases as the reaction continues.
 |
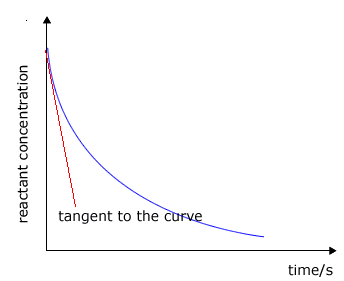The tangent (red line) is the line that just touches the curve and lies at 90º to the radius of curvature. This is not very easy to judge and involves a fair amount of error. |
|
Graph showing the tangent to the curve
|
 |
Once a tangent to the curve has been drawn, the gradient may be found by measuring the difference in the y-value (concentration) divided by the difference in the x-value (time). It makes sense to choose values for the y-axis that give a simple number for the y difference. |
|
Measuring the gradient
|
gradient =
 |
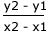To measure the rate, we must make a decision about when to measure it. The only time that we can be certain about the actual concentration of the reactants is at the very beginning of the reaction, so it makes sense to measure the rate at the start. This is called the initial rate of the reaction.
The initial rate is the rate at the start of the reaction.
Average rate
It may not be possible to measure the initial rate for certain reactions, in which case we can choose to measure the average rate over a specific range of the reaction. We do this by timing how long a reaction takes to reach a certain stage.
 |
In this example, the reaction is timed until the concentration of the reactants reaches the value y2. The red line then joins the initial concentration of reactant to the curve at y2. This red line represents the way the concentration would have changed if the rate were constant. The gradient of this line then gives the average rate for the reaction from time 0 to time x2. |
|
average rate graph
|
gradient =
|
The average rate is the rate measured over a certain range of a reaction.
|
Example: The rate of the reaction between sodium thiosuphate and dilute acid may be followed by observing the increased opacity of the solution as it slowly forms a precipitate of sulfur. S2O32-(aq) + 2H+(aq) → H2O(l) + SO2(g) + S(s) If the reaction is performed in a beaker with a mark on the side then the reaction can be timed until the mark is no longer visible through the liquid. The time taken to reach this point is inversely proportional to the average rate. Average rate ∝ 1/t |
Worked examples
Q611-01 Under certain conditions, the average rate of appearance of oxygen gas in the reaction:2O3(g) → 3O2(g)
is 1.2 x 10-3 dm3 sec-1. What is the average rate, expressed in units of dm3 sec-1, for the disappearance of O3?
Answer|
Inspection of the equation shows in the stoichiometry that 2 ozone
molecules produce 3 oxygen molecules. Therefore rate of dissapearance of ozone = 8.0 x 10-4 dm3 sec-1 |
Q611-02 For a specific reaction, A + 2B → 2C + D. The initial rate for the disappearance of reactant A was 2.0 x 10-2 mol dm-3 s-1. What is the initial rate in terms of reactant B, in mol dm-3 s-1?
Answer
|
From the stoichiometry of the equation, one mole of A reacts for every two moles of B, therefore B must react at twice the rate of A. If A has an initial rate of 2.0 x 10-2 mol dm-3 s-1, then B must disappear at a rate of 4.0 x 10-2 mol dm-3 s-1. |
Q611-03 For a specific reaction, AY3 → 3Y + A. The initial rate for the disappearance of reactant AY3 was 2.0 x 10-2 mol dm-3 s-1. What is the initial rate of appearance of product Y, in mol dm-3 s-1?
Answer
|
From the stoichiometry of the equation, one mole of AY3 decomposes and three moles of Y are formed, therefore AY3 must disappear at one third of the rate of the appearance of Y. If the initial rate of decomposition is 2.0 x 10-2 mol dm-3 s-1, then Y must appear at a rate of 6.0 x 10-2 mol dm-3 s-1. |
Q611-04 In a reaction to investigate the decomposition of hydrogen peroxide, 100cm3 of oxygen was collected in exactly 20 seconds. What is the average rate of the reaction in terms of the oxygen gas (cm3 s-1).
Answer
|
100cm3 of oxygen was collected in exactly 20 seconds, therefore 100/20 is collected on average every second = 5 cm-3 s-1 |
Q611-05 In an experiment to determine the effect of temperature on reaction rate, 2-chloropropane was hydrolysed in a water/ethanol mixture according to the equation:
C3H7Cl + H2O → C3H7OH + HCl
and the pH measured electronically. After 10 minutes the pH of a 100cm3 water/ethanol sample had changed from 7.00 to pH 3.00. Calculate the average rate of disappearance of the 2-chloropropane over the first 10 minutes.Answer
|
A solution of pH 3 has a hydrogen ion concentration of 1 x 10-3 mol dm-3 Change in hydrogen ion concentration = 1 x 10-3 mol dm-3 - 1 x 10-7 mol dm-3 = 1 x 10-3 mol dm-3 approximately. From the equation stoichiometry, 1 mole of 2-chloropropane produces 1 mole of HCl Therefore rate of change of 2-chloropropane = 1 x 10-3 mol dm-3 per 10 minutes (600 seconds) Therefore rate of disappearance of 2-chloropropane = 1.67 x 10-6 mol dm-3 s-1 |
Q611-06 If the average rate of a reaction with respect to a reactant A, over the first 100s is 1.2 x 10-3 mol dm-3 s-1, calculate the concentration of A after 100 seconds if the initial concentration of A was 0.2 mol dm-3.
Answer
|
If the average rate = 1.2 x 10-3 mol dm-3 s-1 then there is a decrease in [A] of 1.2 x 10-3 mol dm-3 for every second. Therefore in 100s the decrease in [A] = 100 x 1.2 x 10-3 mol dm-3 = 0.12 mol dm-3 The initial concentration is 0.2 mol dm-3 and the loss is 0.12 mol dm-3 therefore 0.20 - 0.12 Therefore concentration aftrer 100s = 0.08 moles dm-3 |
Q611-07 In an iodine clock reaction the iodine formed in a slow reaction is absorbed by a fixed amount of sodium thiosulfate solution until all the thiosulfate ions are used up. At this point the iodine can form a deep blue/black complex with the starch indicator that is present. If 20cm3 of 0.2 mol dm-3 sodium thiosulfate is used up in 80 seconds, what is the average rate of disappearance of the thiosulfate?
Answer
|
Change in thiosulfate concentration = 0.2 mol dm-3 per 80 s Therefore rate of change of sodium thiosulfate = 2.5 x 10-3 mol dm-3 s-1 |
Q611-08 In the clock reaction in question 7 above the iodine reacts with the sodium thiosulfate according to the equation:
2S2O32- + I2 → S4O62- + I-
What is the average rate of production of iodine in the reaction discussed in question 7?Answer
|
If the average rate of disappearance of the thiosulfate ion is 2.5 x 10-3 mol dm-3 s-1 And the thiosulfate ions react in a ratio of 2 thiosulfate ion to each iodine molecule. Then the rate of appearance of the iodine = rate of disappearance of thiosulfate ions/ 2 = 1.25 x 10-3 mol dm-3 s-1 |
Q611-09 The formation of green cobalt(III) ions in the cobalt(II) catalysed reaction between sodium potassium tartrate and hydrogen peroxide was followed by colorimetry using a calibration curve. After 60 seconds the absorbance of the solution was recorded at 50%. Use the calibration curve below to calculate the average rate over the first 60 seconds.
|
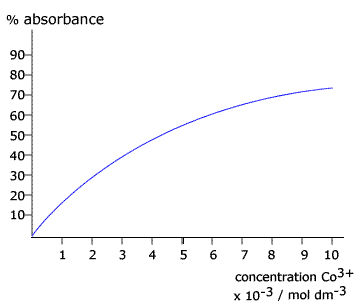
When the absorbance in 50% the concentration of the cobalt 3+ ions is about 4 x 10-3 mol dm-3 Initially the concentration of the cobalt 3+ is zero Therefore in 60 seconds the concentration has changed by 4 x 10-3 mol dm-3. This means that the rate of change of concentration is (4 x 10-3) / 60 = 6.67 x 10-5 mol dm-3 s-1 |
Q611-10 In an experiment to investigate the effect of particle size on rate of reaction, some marble chips were placed in 200cm3 of 2M hydrochloric acid on a balance and readings taken every 10 seconds. The reaction produced carbon dioxide gas and the balance reading fell as the reaction proceeded. After 100 seconds the balance reading had fallen by 2.74g. Use this infomation to calculate the rate of reaction in terms of the concentration of hydrochloric acid over the first 100 seconds.
Answer
|
Mass of carbon dioxide lost = 2.74g Moles of carbon dioxide lost = 2.74/44 moles = 0.0623 moles The equation for the reaction: 2HCl + CaCO3 → CaCl2 + CO2 + H2O, shows us that two moles of HCl react for each mole of CO2 produced. Therefore moles of HCl reacted = 2 x 0.0623 = 0.125 moles These mol of HCl are in 200cm3, therefore the change in concentration of HCl = 0.125/0.2 = 0.623 mol dm-3. This change in concentration happened in 100s, therefore the rate = Δ[HCl]/Δt = 6.2 x 10-3 mol dm-3 s-1. For a longer explanation using concentrations, see below: Initial moles of HCl = molarity x volume = 2 x 0.2 = 0.4 moles Therefore moles remaining after 100s = 0.4 - 0.124 = 0.276 moles This is in 200cm3 therefore the new concentration = 0.276/0.2 = 1.38 mol dm-3 Therefore the change in concentration = 2.00 - 1.38 = 0.62 mol dm-3 This occurred in 100 seconds so the rate of change of concentration = 0.62/100 = 6.2 x 10-3 mol dm-3 s-1 |