The term "order" refers to the value of the exponential in a formula. It is the power to which a value has been raised. 102 = 100. The order of 10 = 2
Syllabus reference R2.2.10
Reactivity 2.2.10 - The order of a reaction with respect to a reactant is the exponent to which the concentration of the reactant is raised in the rate equation. (HL)
- The order with respect to a reactant can describe the number of particles taking part in the rate-determining step.
- The overall reaction order is the sum of the orders with respect to each reactant.
- Sketch, identify and analyse graphical representations of zero, first and second order reactions.
Guidance
- Concentration–time and rate–concentration graphs should be included.
- Only integer values for order of reaction will be assessed.
Tools and links
- Tool 1, Tool 3, Inquiry 2 - What measurements are needed to deduce the order of reaction for a specific reactant?
- Nature of science - Why are reaction mechanisms only considered as “possible mechanisms”?
The order of a function
All relationships between two variables can be represented by an equation.
This would be the equation for the graph obtained showing how the two factors
vary with one another.
There are only three logical possibilities for a relationship between two variables,
for example A and B.
- 1 No relationship at all - Change in A
does not affect B
- 2 A directly proportional relationship -
Change in A causes a corresponding change in B
- 3 A relationship that is not directly
proportional - Change in A causes a non-linear change in B
 |
|
dependency of rate on concentration
|
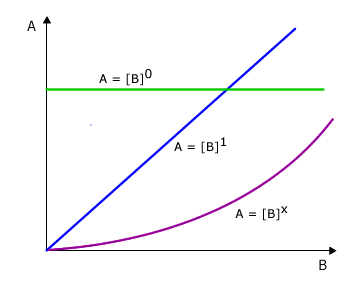
All of these possible relationships can be covered by the simple mathematical
formula A = Bx
Possibility 1: No relationship at all
In this case the value of x is zero and the equation becomes A = B0
Any number raised to the power of zero = 1 so the equation reduces to A = 1,
in other words there is no change in the value of B when A changes.
Possibility 2: Direct proportionality
In this case the value of x = 1 and the equation reduces to A = B1
Any number raised to the power of 1 is that number itself (eg: 21
= 2, 31 = 3, etc). In other words when A changes this causes a change
by exactly the same factor in B. For example, if the value of A doubles then
the value of B must double also.
Possibility 3: Some other relationship
In this case the value for x is some other number apart from 0 or 1. The value
of x depends on the manner in which B changes with change in A. For the time
being let's leave it as the unknown value 'x'.
Possible relationships between A and B
^ top
Worked examples
Q633-01 A proposed mechanism
for the reaction 2NO(g) + Br
2(g)
→ 2NOBr(g) is as follows:
NO(g) + Br2(g) → NOBr2(g) slow
NO(g) + NOBr2(g) → 2NOBr(g) fast
If this mechanism is correct then the rate law could be expected to be which
of the following:
- rate = k[NO][Br2]
- rate = k[NO]2[Br2]
- rate = k[NO][NOBr2]
- rate = k[NO]2
Answer
|
It can be seen that in the slow (rate determining) step of the reaction
one molecule of NO collides with one molecule of Br2. We
would expect that the order of each of these reactants is 1.
Rate = k [NO]1[Br2]1
|
Q633-02 The rate of the reaction
2A + B
→
Products, is consistent with the rate equation, rate = k[A][B].
Which reaction mechanism is consistent with this information?
| A. |
A + B →
AB (slow) |
| |
AB + A →
Products (fast) |
| B. |
A + A →
A2 (slow) |
| |
A2 + B →
Products (fast) |
| D. |
A + A →
A2 (fast) |
| |
A2 + B →
Products (slow) |
Answer
|
The order of the concentrations in the rate equation suggests the molecularity
of these particles in the rate-determining step (in addition to equilibria
or previous reactions that feed new particles into the rate determining
step)
Only mechanism (A) has one particle of A and one of B in the rate determining
step.
|
Q633-03 The following reaction,
X
2(g) + 2Y(g)
→
2XY(g), has the proposed mechanism:
X2 →
2X slow
X + Y →
XY fast
Based on this information the rate expression for this reaction is:
- rate = k[XY]
- rate = k[X2][Y]2
- rate = k[X2]
- rate = k[2X]
Answer
|
The first step is rate determining and involves only the decomposition
of X2 molecules. The rate expression can only reflect this fact:
rate = k[X2]
|
Q633-04 The reaction of hydrogen
and iodine monochloride is represented by this equation.
H2(g) + 2ICl(g) → 2HCl(g) + I2(g)
This reaction is first order in H2(g) and also first order in ICl(g). Which
of these proposed mechanisms can be consistent with the given information about
this reaction?
| Mechanism 1 |
H2(g) + 2ICl(g) → 2HCl(g) + I2(g) |
|
| Mechanism 2 |
H2(g) + ICl(g) → HCl(g) + HI(g) |
slow |
| |
HI(g) + ICl(g) → HCl(g)
+ I2(g) |
fast |
- 1 only
- 2 only
- Both 1 and 2
- Neither 1 nor 2
Answer
|
First order in H2(g) and also first order in ICl(g) suggests that one
molecule of each of the species are involved in rate determining processes.
In mechanism 1 there appears to be a three particle collision, making
it extremely improbable. In mechanism II the collision is between one
molecule of H2 and one of ICl in the slow (rate determining
) step. Thus only mechanism 2 is a
possibility.
|
Q633-05 For the hypothetical
reaction 2X + 2G
→ Q + 2M,
the rate expression is Rate = k[X]
2[G]. Which mechanism is most likely?
| A. |
2X + G ⇋
2Q + R (fast equilibrium) |
| |
Q + R + G → 2 M (slow,
rate determining) |
| B. |
X + G ⇋
Q + R (fast equilibrium) |
| |
R + X → 2M (slow,
rate determining) |
| C. |
X + X ⇋
X2 (fast equilibrium) |
| |
X2 + G → Q + T (slow, rate determining) |
| |
T + G → 2M (fast)
|
| D. |
G + G ⇋
G2 (fast equilibrium) |
| |
G2 + X → Q + T (slow, rate determining) |
| |
T + X → 2M (fast)
|
Answer
|
For a hypothetical mechanism to be valid it must fulfil three conditions:
- Firstly the sum of all of the steps must give the stoichiometric
equation.
- Secondly the orders of the reactants must coincide with the particle
collisions involved in the slowest step and steps leading into the
slowest step.
- Thirdly, there must be no three-particle collisions.
Mechanism A can be discarded as both steps involve three-particle collisions.
Mechanism B does not add up to the stoichiometric equation overall
and so cannot be possible.
Mechanism C has no three-particle collisions, the sum of all of the
equations add up to the stoichiometric reaction equation and the orders
of the components in the rate expression suggest that there should be
two particles of X and one particle of G in the slowest step, or in
the showest step plus steps leading into the slowest step. This is the
case, as step 1 has two particles of X, and this leads into the second
(slow) step, which has one particle of G. The answer is response
C.
Mechanism D would have a rate expression with orders of reaction of
two with respect to G and one with respect to X.
|
Q633-06 The reaction between
chloroform, CHCl
3(g), and chlorine, Cl
2(g), to form CCl
4(g)
and HCl(g) is believed to occur by this series of steps.
- Step 1: Cl2 → Cl(g) + Cl(g)
- Step 2: CHCl3(g) + Cl(g) → CCl3(g) + HCl(g)
- Step 3: CCl3(g) + Cl(g) → CCl4(g)
If this reaction is first order in CHCl3 and half order in Cl2,
which statement about the relative rates of step 1, 2, and 3 is correct?
- Step 1 is the slowest.
- Steps 1 and 2 must both be slow.
- Step 2 must be slower than step 1.
- Step 3 must be the slowest
Answer
|
As the order of reaction with respect to CHCl3 is one, one
molecule of this would be expected to figure in the slowest step. This
is also backed up by a faster equilibrium leading into step 2 as chlorine
also is involved in the rate expression, albeit with a fractional rate.
Hence, step 2 must be slower than step 1.
|
Q633-07 The mechanism for the
decomposition of nitrogen(V) oxide, has been identified as follows:
|
k1
N2O5 → NO2 + NO3 (slow)
|
|
k2
NO2 + NO3 → NO2 + O2 + NO (fast)
|
|
k3
NO + N2O5 → 3NO2 (fast)
|
The stoichiometric equation for this decomposition is:
- N2O5 → NO2
+ NO2
- N2O5 → NO2
+ O2 + NO
- 2N2O5 → 4NO2 +
O2
- N2O5 + NO → 3NO2
Answer
|
The stoichiometry is obtained by adding all of the equations and cancelling
out the same substances from each side.
|
N2O5 → NO2 + NO3 (slow)
|
|
NO2 + NO3 → NO2 + O2 + NO (fast)
|
|
NO + N2O5 → 3NO2 (fast)
|
| N2O5 + NO2
+ NO3 + NO
+ N2O5 → NO2 + NO3 + NO2
+ O2 + NO + 3NO2
|
|
2N2O5
→ 4NO2
+ O2
|
|
Q633-08 The rate law consistent
with the mechanism shown in question 07 above is:
- rate = k1 [N2O5]
- rate = K3 [NO][N2O5]
- rate = k1k2k3 [N2O5]2
- rate = k2 [NO2][NO3]
Answer
|
As only N2O5 is involved in the slowest step
and nothing leads into this step, the only reactant that should appear
in the rate expression is N2O5.
Therefore response A, rate = k1
[N2O5] seems most likely.
|
Q633-09 For the stoichiometric
reaction:
| CHCl3(g) + Cl2(g) → CCl4(g) + HCl(g) |
the rate law, rate = k[CHCl3][Cl2]1/2 has
been determined. The mechanism given below has been proposed.
- step 1: Cl2 ⇋
2Cl
- step 2: CHCl3 + Cl → CCl3 + HCl
- step 3: CCl3 + Cl → CCl4
For this reaction, the rate determining step must be:
- step 1.
- step 2.
- step 3
- 1/2 times step 1
Answer
|
Chlorine appears in the rate expression and so does CHCl3.
If step 2 were the slowest step with step 1 feeding into it then
this would give the particles in the rate expression.
Therefore step 2 is the slowest.
|
Q633-10 The ionic reaction:
| 3I- + S2O82- → 2SO42- + I3- |
is found to be described by the experimental rate equation, rate = k[I-]
[S2O82-]. This suggests that:
- the reaction occurs when three iodide ions collide simultaneous with one
S2O82- ion
- there must be only one step in the overall reaction since the rate is first-order
in both reactants
- the rate of reaction is inhibited by the presence of I3-
- a slow step in the overall reaction sequence may involve the collision of
a single I- ion with a single S2O82-
ion.
Answer
|
The rate expression suggests a collision between one iodide ion and
one peroxodisulfate ion in the slowest step, as the order with respect
to each of these components is 1. Response
D.
|
^ top
