IB Colourful Solutions in Chemistry

Higher-level only

Calculations involving weak acids and bases are conditioned by the fact that the acid (or base) does not dissociate 100% into ions. This must be taken into account.

Syllabus ref: R3.1.10

Reactivity 3.1.10 - The strengths of weak acids and bases are described by their Ka, Kb, pKa or pKb values. (HL)

Interpret the relative strengths of acids and bases from these data.

Guidance

Tools and links

The acid dissociation constant
pKa values
The base dissociation constant
Conjugate acids
Multiplying Ka and Kb
Worked examples
Now test yourself

The acid dissociation constant

The acid dissociation constant, Ka, comes from the equilibrium constant for the breakdown of an acid in aqueous solution:

HA + H₂O ⇋ A^- + H₃O⁺

Where H₃O⁺ is the hydrogen ion is solution, it may also be written H⁺(aq). The equilibrium law for this dissociation is:

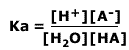
As the concentration of water is effectively constant, a new constant, the acid dissociation constant, Ka, is defined as:

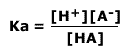
The acid dissociation constant, Ka gives a measure of the extent of the dissociation. If Ka is a large value then the acid is strong and dissociates into ions easily. These constants are only useful for weak acids.

Acid	Ka
Methanoic acid	1.78 x 10^-4
Ethanoic acid	1.74 x 10^-5
Propanoic acid	1.35 x 10^-5
Butanoic acid	1.51 x 10^-5
Hydrocyanic acid	3.98 x 10^-10
Hydrofluoric acid	5.62 x 10^-4
Carbonic acid	4.26 x 10^-7

From the list it may be seen that methanoic acid is a stronger acid than ethanoic acid, i.e. it dissociates further releasing more hydrogen ions in solution.

Example: Hydrogen ion concentration from Ka.
Calculate the [H+(aq)] of 0.2 M ethanoic acid (Ka = 1.78 x 10^-5)

Ethanoic acid is a weak acid. It only partially dissociates according to the equation:

CH₃COOH ⇋ CH₃COO^- + H⁺

Therefore the acid dissociation constant:

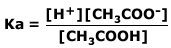
We can assume that as the acid only slightly dissociates then the concentration of the acid at equilibrium is the same (to a close approximation) as the concentration of the original acid (in this case = 0,2 M)

Therefore:

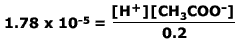
And as the hydrogen ion concentration equals the ethanoate ion concentration, then:

0.2 x 1.78 x 10^-5 = [H⁺]²

[H⁺] = √ (3.56 x 10^-6)

[H⁺] =1.89 x 10^-3

^ top

pKa values

The pKa values give us a convenient measure of the acid strength. The lower the value the stronger the acid. The pKa value depends on the ease of breakdown of the acid molecule as well as the stability of the ions formed and their relative hydration energies.

The carboxylic acids show a trend over the first three members that is broken with the fourth. The trend from methanoic acid to propanoic acid may be explained by the inductive effect of the alkyl group increasing the electron density in the O-H bond. The reversal of the trend with butanoic acid is possibly due to the lower solubility of the larger hydrocarbon chain of the ion, with corresponding lower hydration enthalpy.

Acid	pKa
Methanoic acid	3.75
Ethanoic acid	4.76
Propanoic acid	4.87
Butanoic acid	4.82
Hydrocyanic acid	9.4
Hydrofluoric acid	3.25
Carbonic acid	6.37

In this instance you can see that the SMALLER pKa values correspond to the stronger acids. Methanoic acid has a SMALLER pKa value, therefore it is a stronger acid than ethanoic acid.

QC853: pKa and Ka of weak acids

Your Answer

^ top

The base dissociation constant

When bases interact with water they do so by removing a hydrogen ion creating hydroxide ions in solution.

NH₃ (aq) + H₂O ⇋ NH₄⁺(aq) + OH^-(aq)

Once again, the water concentration is effectively constant and allows us to define a new constant, Kb:

Kb is referred to as the base equilibrium constant and gives a measure of the extent of the equilibrium. Large values for Kb means strong base. However, as for acids, the values are usually very small and the -log(10) form of the information is used to generate convenient sized numbers.

pKb = - log₍₁₀₎ Kb

The lower the pKb value the stronger the base.

^ top

Conjugate acids

With bases it may be more convenient to use the conjugate acid of the base to define a new Ka value, this time for the reverse reaction. In the ammonia base equilibrium above, the conjugate acid is the ammonium ion, NH₄⁺, whose dissociation proceeds according to the following equation:

NH₄⁺ + H₂O ⇋ NH₃ + H₃O⁺

For which the acid dissociation constant is:

This allows us to have a pKa value for a specified base, although it is actually the pKa value of the conjugate acid of the base.

^ top

Multiplying Ka and Kb

If the Kb value of a base is multiplied by the Ka value of its conjugate acid we get the following:

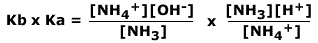
Cancelling out the same terms:

Rearrange:

And we already know that [H⁺][OH-] = Kw = 1.0 x 10^-14, therefore:

Take logs and change the sign throughout:

pKa + pKb = pH + pOH = pKw = 14

The following relationships exist:

pKa + pKb = 14
pH + pOH = 14
pH = 14 - pOH
pKa = 14 - pKb
pKw = pKa + pKb
Ka x Kb = Kw

These equations allows us to manipulate acid and base equilibrium constant values very easily.

^ top

Worked examples

Q853-01 Benzene carboxylic (benzoic) acid has a Ka = 6.6 x 10^-5. What is the pH of a 0.30 M aqueous solution of benzene carboxylic acid?

0.52
2.4
4.2
4.7

Answer

For the weak acid equilibrium HA H+ + A-

Assuming that the [HA] is the same at equilibrium as in the beginning, and observing that [H+] = [A-] from the equation stoichiometry:

6.6 x 10^-5 = [H+][A-]/[0.3]

0.3 x 6.6 x 10^-5 = [H+]2

[H+] = 4.45 x 10^-3

pH = -log[H+] = 2.35

Q853-02 What is the relationship between Ka and pKa?

pKa = -logKa
pKa = 1.0 x 10^-14 Ka
pKa = logKa
pKa = 1.0 Ka

Answer

The letter 'p' means the negative log of the following constant, ∴pKa = -log(10)Ka

Response A

Q853-03 If a weak monoprotic acid is 5.0% dissociated in a 0.10 M aqueous solution of the acid, what is the acid equilibrium constant, Ka, for this acid?

2.5 x 10^-5
2.5 x 10^-4
5.0 x 10^-3
5.0 x 10^-2

Answer

For the weak acid equilibrium HA H+ + A-

5% dissociated means that only 5% of the acids molecules turn to ions (leaving 95% undissociated)

	HA	H+	+	A-
initially moles	0.1	0		0
@ equilibrium	0.095	0.005		0.005

Ka = [0.005][0.005]/[0.095]

Ka = 2.63 x 10^-4

If we assume the approximation for the IB that the acid concentration is the same at equilibrium then this becomes

Ka = [0.005][0.005]/[0.1]

Ka = 2.5 x 10^-4

Q853-04 What are the [H+] and [OH^-] in a 0.10 mol dm^-3 solution of a weak acid (Ka = 1.0 x 10^-3)?

	[H+]	[OH^-]
A	1.0 x 10^-1	1.0 x 10^-13
B	1.0 x 10^-3	1.0 x 10^-11
C	1.0 x 10^-2	1.0 x 10^-12
D	1.0 x 10^-6	1.0 x 10^-8

Answer

For the weak acid:

Assume [HA] to be unchanged = 0.10 mol dm^-3

And [H+] = [A^-]

Therefore [H+] = √(Ka x 0.1)

Therefore [H+] = 1.0 x 10^-2 mol dm^-3

And as [H+] x [OH^-] = 1.0 x 10^-14

Therefore [OH^-] = 1.0 x 10^-12 mol dm^-3

Q853-05 The Ka value for an acid is 1.0 x 10^-2. What is the Kb value for its conjugate base?

1.0 x 10^-2
1.0 x 10^-6
1.0 x 10^-10
1.0 x 10^-12

Answer

Ka and Kb are connected by the relationship: Ka + Kb = 1.0 x 10^-14

Therefore if Ka = 1.0 x 10^-2, then Kb = 1.0 x 10^-12

Q853-06 What is the Ka of a 0.10 mol dm^-3 solution of a weak monoprotic acid if the [H+] = 2.0 x 10^-3 mol dm^-3?

2.0 x 10^-2 mol dm^-3
2.0 x 10^-4 mol dm^-3
4.0 x 10^-5 mol dm^-3
4.0 x 10^-7 mol dm^-3

Answer

The acid dissociation constant is given by:

And [H+] = [A^-]

Therefore this could be written as:

Therefore when [HA] = 0.10 mol dm^-3 and [H+] = 2.0 x 10^-3 mol dm^-3

Ka = 4.0 x 10^-5

Q853-07 A 0.1 mol dm^-3 solution of a weak acid has a pH of 3.0. What is Ka for this acid?

1 x 10^-1
1 x 10^-3
1 x 10^-5
1 x 10^-6

Answer

The acid dissociation constant is given by:

The relationship between pH and [H+] is:

When pH = 3 the hydrogen ion concentration = 1 x 10^-3 mol dm^-3

As [H+] = [A^-] we can write the expression as:

∴ Ka = (1 x 10^-3)²/0.1 = 1 x 10^-5

Q853-08 Find the concentration of an ethanoic acid solution whose pH is measured at 3.5 (Ka = 1.78 x 10^-5)
Answer

The acid dissociation constant is given by:

The relationship between pH and [H+] is:

When pH = 3.5 the hydrogen ion concentration = 3.16 x 10^-4 mol dm^-3

As [H+] = [A^-] we can write the acid dissociation expression as:

Rearranging:

Therefore the concentration of ethanoic acid = 5.6 x 10^-3 mol dm^-3

Q853-09 The pH of a solution of vinegar is 3.00. The concentration of OH^- ion in this solution is

3.00 M
1 x 10^-3 M
1 x 10^-11 M
17 M

Answer

From the molarity of the acid [H⁺] = 1 x 10^-3

and Kw = [H⁺][OH^-] = 1 x 10^-14

Therefore [OH^-] = 1 x 10^-11 mol dm^-3

Q853-10 25cm³ of a 0.1 mol dm^-3 solution of hydrochloric acid reacts with 75cm³ of a 0.10 mol dm^-3 solution of sodium hydroxide. Calculate the pH of the final solution.
Answer

25cm³ of a 0.1 mol dm^-3 solution of hydrochloric acid = 0.025 x 0.1 moles = 0.0025 moles HCl

75cm³ of a 0.10 mol dm^-3 solution of sodium hydroxide = 0.075 x 0.10 moles = 0.0075 moles NaOH

Equation for the reaction: NaOH + HCl → NaCl + H₂O

Thus all of the acid is neutralised and 0.0075 - 0.0025 moles of NaOH remain = 0.005 moles NaOH.

Total volume of solution after mixing = 25cm³ + 75cm³ = 100cm³

Therefore molarity of the final solution = 0.005/0.1 mol dm^-3 = 0.05 mol dm^-3 NaOH solution

Sodium hydroxide is a strong base and completely dissociated so [OH^-] = 0.05 mol dm^-3

pOH = -log[OH^-] = 1.30

pH + pOH = 14

Therefore pH = 14 - 1.30 = 12.7

Now test yourself

^ top