Standard level
If the number of moles present in a gas and its mass is known, then the relative molecular mass of a gas can be calculated.
Syllabus ref: S1.5.4Structure 1.5.4 - The relationship between the pressure, volume, temperature and amount of an ideal gas is shown in the ideal gas equation PV = nRT and the combined gas law P1V1/T1= P2V2/T2.
- Solve problems relating to the ideal gas equation.
Guidance
- Units of volume and pressure should be SI only. The value of the gas constant R, the ideal gas equation, and the combined gas law, are given in the data booklet.
Tools and links
- Tool 1, Inquiry 2 - How can the ideal gas law be used to calculate the molar mass of a gas from experimental data?

Ideal gas equation
The equation of state refers to a fixed mass of gas. From Avogadro's law we know that the same volume of all gases contain the same number of moles and from this, it follows that the volume is proportional to the number of moles.
Volume ∝ number of moles (n)
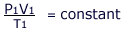
These two equations can be combined to obtain an expression involving all the quantities:
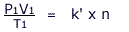
After rearrangement, for 'n' moles of gas the proportionality constant is called the Universal Gas Constant and is given the symbol 'R'
This gives the ideal gas equation:
Ideal Gas Equation: PV = nRT
where:
- P = pressure in Pa
- V = volume in m3
- n = number of moles of gas
- R = Universal Gas constant = 8.314 JK-1mol-1
- T = the absolute temperature in Kelvin
It is often more convenient to express the pressure in kPa and the volume in litres (dm3). This leaves the value of R the same (see below).
|
Example: Calculate the number of moles of gas present in 2.6 dm3 at a pressure of 1.01 x 105 Pa and 300 K. PV = nRT 2.6 dm3 = 0.0026 m3 0.0026 x 1.01 x 105 = n x 8.314 x 300 n = 0.0026 x 1.01 x 105 / 8.314 x 300 n = 0.105 moles |
There are several units used for gas volume, gas pressure and temperature. It is important to be consistent with the use of units when carrying out gas law calculations. The Syllabus states that SI units will be used wherever possible.
Universal gas constant - R
Although called "Universal", its value depends on the units used for P, V and T.
With the SI units of metres, kilograms, Kelvin and Joules, using P, V and T values at STP gives:
| PV=nRT | |
| therefore: | R=PV/nT |
| for 1 mole of gas at STP (using accepted values of P = 1.00 x 105 Pa, V = 0.02271 m3, T = 273.15 K) | |
| R = | (1.00 x 105) x 0.02271)/273.15 |
| R = | 8.314 J K-1 mol-1 |
In chemistry, the units of volume used are the decimetre cubed (dm3) and pressure in kiloPascals (kPa), so one unit is 100x greater and the other 100x smaller than the SI equivalent. Consequently the differences in the product, PV, both cancel out (multiplying AND dividing by 1000), so that the final value for R is the same as in SI units.
The Universal gas constant, R, calculated using atmospheres Pressure and volume in litres, then:
| PV=nRT | |
| R=PV/nT | |
| at STP: | P = 1 atm, V = 22.7 dm3, T = 273 |
| n = 1 | |
| R = 0.0821 dm3 atm mol-1 K-1 |
There are, of course, several other values of R, as there are several ways of measuring both the volume and the pressure of a gas.
SI units and 'R'
The SI units of P, V and T give rise to the previously used value for the universal gas constant, R = 8.314 J K-1 mol-1.
How does this happen when chemists do not use these SI units?
Remember:
1 litre = 1 dm3 = 1000 cm3
Consequently, if litres are used in the Ideal Gas equation then the pressure units must also be divided by 1000 (as PV = constant). Pressure is measured in Pa or Nm-1, and so the unit of the kPa correct for the difference in volume units.
Atmospheric pressure in Pa = 1.00 x 105 Pa
Atmospheric pressure in kPa = 1.00 x 102 kPa
Provided that you are consistent with the application of units there will be no problem. It is always a good idea when carrying out calculations to look at the value of your answer and ask yourself, "does it seem reasonable?"
Worked examples
Q154-01 What volume is needed to store 50 moles of an ideal gas at 15 atmospheres and 25 ºC?|
PV = nRT Convert pressure to kPa and temperature to Kelvin. P = (15 x 100) = 1500 kPa, n = 50 mol, T = (273 + 25) = 298 K, R = 8.314 J K-1 mol-1 V = nRT/P = (50 x 8.314 x 298)/1500 Therefore volume needed = 82.6 dm3 |
Q154-02 What pressure will be exerted by 200 moles of hydrogen gas in a 7.5L cylinder at 20ºC?
|
PV = nRT Convert temperature to Kelvin. V = 7.5 dm3, n = 200 moles, T = (273 + 20) = 293 K, Pressure exerted = (200 x 8.314 x 293)/7.5 Therefore pressure exerted = 64960 kPa |
Q154-03 The temperature in Kelvin of 2 dm3 of an ideal gas is doubled and its pressure is increased by a factor of 4. Calculate the final volume of the gas.
|
The ideal gas equation: PV = nRT Shows that when the temperature is doubled so the value of the volume must double also, ie a twofold increase (initial volume x 2). However, when nRT is constant, a fourfold increase in pressure results in a fourfold (x4) decrease in volume (= initial volume/4) Combining the two effects (that of the temperature and the pressure change) the volume increases by a factor of 2 and decreases by a factor of 4 (volume = initial volume x 2/4) Therefore the overall change in gas volume is a twofold decrease (volume = initial volume/2) Final volume is therefore 2/2 = 1 dm3 |
Q154-04 Calculate the volume occupied by 0.01 moles of hydrogen gas at 20ºC and atmospheric pressure.
|
Gas molar volume at STP = 22.7 dm3 0.01 moles of gas occupies 0.01 x 22.7 = 0.227 dm3 20ºC is equivalent to 20 + 273 K = 293 K Using V1/T1 = V2/T2 (where V1 and T1 are under STP conditions) 0.227/273 = V2/293 Therefore V2 = (0.227 x 293)/273 = 0.2436 dm3 = 243.6 cm3 Therefore 0.01 moles of hydrogen occupies 243.6 cm3 at 20ºC |
Q154-05 How many moles of gas are present in a gas volume of 24 dm3 at 100ºC and atmospheric pressure?
|
Using the ideal gas equation PV=nRT 100ºC = 373K, R = 8.314, atmospheric pressure = 100 kPa n = PV/RT= (100 x 24)/(8.314 x 373) n = 0.774 moles |
Q154-06 For which set of conditions does a fixed mass of an ideal gas have the greatest volume?
|
Temperature
|
Pressure
|
|
|
A
|
low
|
low
|
|
B
|
low
|
high
|
|
C
|
high
|
high
|
|
D
|
high
|
low
|
|
From the ideal gas equation, PV = nRT When T is high, V must also be high but as nRT is equal to a constant value, any increase in P must cause a decrease in V Therefore V is high when P is low. Correct response = D |
Q154-07 A 0.450g sample of gaseous aluminium chloride occupies a volume of 51.2 cm3 at 100ºC and 102 kPa. Calculate its relative molecular mass.
|
100ºC is equivalent to 373K, 51.2 cm3 = 0.0512 dm3 Using PV=nRT, n = PV/RT n = (102 x 0.0512)/(8.314 x 373) n = 1.684 x 10-3 The mass of 1.684 x 10-3 moles = 0.450 g Therefore the mass of 1 mole = 0.450/1.684 x 10-3 = 267 The relative molecular mass of aluminium chloride = 267 Note: The formula of aluminium chloride is AlCl3, however this gives a relative formula mass of 27 +(3 x 35.5) = 133.5 exactly half the calculated value. The Mr value produced in the above calculation suggests that the correct formula of aluminium chloride is 2 x AlCl3 or Al2Cl6 |
Q154-08 Calculate the number of moles of helium in a weather balloon measuring 200 m3 at 5ºC and 80 kPa pressure.
|
Using PV=nRT n=PV/RT Volume = 200 m3 = 2 x 105 dm3 Number of moles of helium = (80 x 2 x 105 )/(8.314 x 278) Therefore the number of moles of helium = 6923 moles (to 4 significant figures) |
Q154-09 The molar mass of an unknown gas is to be determined by weighing a sample. As well as its mass which of the following must be known.
- I. Pressure
- II. Temperature
- III. Volume
- I only
- II only
- I and II only
- I, II, and III
|
To calculate the molar mass of a gas the number of moles must be known as well as the mass of gas to use the relationship: Molar mass = Mass/moles The number of moles is obtained from PV=nRT Therefore the Pressure, Volume and Temperature must be known. Correct response = D |
Q154-10 In an experiment to determine the relative molecular mass of an unknown hydrocarbon, 0.15 g of the liquid hydrocarbon was injected through a rubber septum into a gas syringe. The gas syringe was placed in an oven at 120ºC and left to reach equilibrium. The final volume occupied by the vapour in the syringe was measured and found to be 67.4 cm3. Calculate the relative molecular mass of the hydrocarbon, if the atmospheric pressure was 101 kPa on that day.
|
Temperature 120ºC is equal to 120 + 273 = 393K Volume 67.4 cm3 = 0.0674 dm3 Using PV = nRT n = PV/RT n = (101 x 0.0674)/(8.314 x 393) = 2.083 x 10-3 This number of moles has a mass = 0.15 g Therefore mass of 1 mole = 0.15/ (2.083 x 10-3) = 72 Therefore the relative molecular mass of the hydrocarbon = 72 |
Now test yourself
External video resources
Combined gas law problems: Richard Thornley