|
One of the most fundamental characteristics of the mass spectrometer is its ability to determine relative atomic masses from isotopic abundances.
|
|
Relative mass
The term relative atomic mass refers to the average mass of an atom of a specific element as compared to the 12 carbon isotope (equal to 12.0000 atomic mass units)
To calculate relative atomic masses from isotopic data you need:
- The relative mass of each isotope
- The percentage abundance of each isotope
With this data, relative mass calculation is a simple affair:
|
RAM =
|
(mass of isotope1 x % abundance isotope1) + (mass of isotope2 x % abundance isotope2) |
|
100
|
|
Example: Boron has two isotopes Boron-10 and Boron-11 which have relative abundancies of 20% and 80% respectively. In 100 atoms there are 20 Boron atoms with a mass of 10 and 80 Boron atoms with a mass of 11 Total mass of the boron atoms is:- (20 x 10) + (80 x 11) = 1080 Therefore the average mass of 1 atom is = 10.80 Boron has a relative atomic mass of 10.80 |
Mr determination from MS
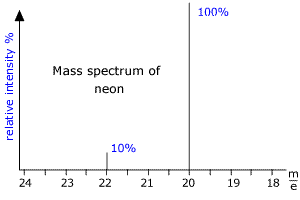 |
Here we can see that there are two peaks in the mass spectrum, one at m/e (this means mass to charge ratio) = 20 and the other at m/e = 22. These peaks correspond to the ions produced from the diferent isotopes of Neon. As neon has two common isotopes 20Ne and 22Ne, any naturally occurring sample of neon will contain these two isotopes. The mass spectrum shows that the peaks are in the ratio 10:1 and so there is 10 times as much 20Ne as 22Ne in the sample. From this data the relative atomic mass of neon can be calculated. RAM = [(10 x 20) + (1 x 22)]/11 = 20.2 |

