| Hess' law emerges as a logical consequence of the law of conservation of energy. |
|
Energy cycles
Hess' law tells us that any difference in energy converting between two substances is independent of the route taken for the conversion.
An energy cycle is a diagram showing how three, or more reactions are interconvertable. Energy cycles can be constructed to find unknown energy changes, by adding up the energies of steps from a different route to the same final products.
For example, if the energy of the conversion A ![]() B is known, and C can also be converted into B, C
B is known, and C can also be converted into B, C ![]() B, and this energy change is also known, then an energy cycle can be constructed
to allow us to find the energy change of A
B, and this energy change is also known, then an energy cycle can be constructed
to allow us to find the energy change of A ![]() B, or B
B, or B ![]() A.
A.
To construct an energy cycle to find an unnown enthalpy change, the following two conditions must be satisfied:
- Two of the equations have the same products.
- Two out of three equations have a known energy change
Constructing energy cycles
Energy cycles can be constructed from any equations in which the products (or the reactants) are the same. For example, if two separate equations give the same products:
|
equation 1 A equation 2 C |
Then we can safely state that the energy change of the route from A to C is a function of the two energy changes, A to B and C to B. When constructing the cycle you MUST keep the arrows indicating direction of change in the correct orientation with respect to each pair of reactants and products.
REM It is very important to take notice of the direction of the arrows when constructing the cycle. If you are going in the same direction as the arrow then there is no change to the energy, however if you are moving in a direction opposed to the direction of the arrow then you must reverse the sign of the energy change.
In the example above, to move from A to C via B there are two steps:
|
step 1: A step 2: B |
Notice that this second step involves moving against the direction of the arrow, so in the final calculation the energy change sign is reversed. However, the energy cycle MUST be constructed while remaining faithful to the directions of the original arrows.
Constructing cycles with different stoichiometry
The previous example assumed that the stoichiometery of the equations matched perfectly. But what do you do when the equations just dont add up? In that case we just manipulate the equations mathematically so that they do add up BEFORE constructing the Hess' cycle.
Let's suppose that we are given two equations with the same product but different number of moles, as seen by the coefficient in the equation:
|
equation 1 A equation 2 C |
Before constructing the energy cycle we must make sure that the number of moles of the common factor (in this case 'B') are the same. So to do this we multiply through by 2 in equation 1, remembering to do the same to the value of the energy. This gives:
|
2A C |
And the Hess energy cycle is constructed as before.
Example: In the preparation of sulfuric acid,
sulfur is converted to sulfur dioxide by burning in oxygen:
The sulfur(IV) oxide is then converted into sulfur (VI) oxide by passing, with more oxygen, over a vanadium (V) oxide catalyst:
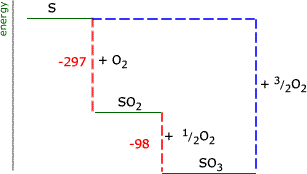
Note this reaction shows two moles of sulfur(IV) oxide. The energy change for 1 mole is half this value = -98 kJ. It is not possible to carry out the reaction between oxygen and sulfur to make sulfur(VI) oxide directly. However, an energy cycle can be drawn that allows us to find the energy change that would occur if it were possible. The above cycle shows us that there are two routes to sulfur(VI) oxide from sulfur. One route is direct (for which we don't know the energy) and the other route is via sulfur(IV) oxide. The energy change for both routes is the same. ΔH(S + O2 -297 - 98 = ΔH(S + ∴ ΔH for the conversion of sulfur to sulfur (VI) oxide = -395 kJ |
Enthalpy level diagrams
When a Hess' law energy cycle is presented graphically showing the relative chemical energies of the reactants and products, this is called an energy, or enthalpy level diagram. Personally, I find these more logical than Hess' energy cycles, however it's a matter of individual preference.
If we represent the above example of the sulfur oxides on an energy level diagram, we must take into account the signs of the energy changes. Remember that a negative sign indicates that chemical energy is being converted into heat energy and the chemical energy goes down. The products of an exothermic reaction are lower on the graph than the reactants.
|
The energy cycle at the right shows us the unknown route as a blue dashed line. It is apparent that this is equal in magnitude to the sum of the two red dashed lines. ΔH(reaction) = -297 + (-98) = -395 kJ |
 |
|
Example: Draw an enthalpy level diagram to represent the following transformations and use it to calculate the enthalpy of formation of phosphorus trichloride (reaction 1):
Note that in equation 3 there are two moles of phosphorus. The energy change must be adjusted to show the transformation for 1 mole of phosphorus: 4 P(s) +
In this case, the red dotted line is obtained by subtracting the small blue dotted line from the longer blue dotted line. That is, the enthalpy of 4 - 2 = -463 - (-124) = -339 kJ Therefore the standard enthalpy of formation, ΔHf |

 = -297 kJ mol-1
= -297 kJ mol-1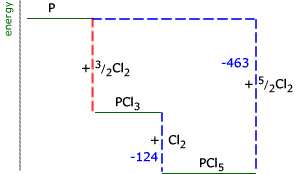 The
enthalpy level diagram can now be constructed.
The
enthalpy level diagram can now be constructed.