|
The rate equation is a general formula that relates the rate of a chemical reaction to the concentration of the reacting species. Each individual reaction has its own rate equation that must be determined by experiment. |
Rate = k[A]x[B]y |
Relationship between rate and concentration
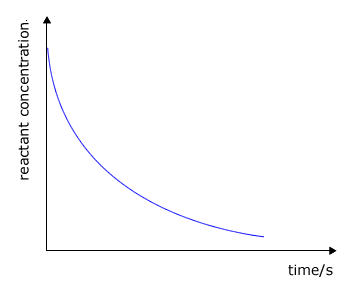
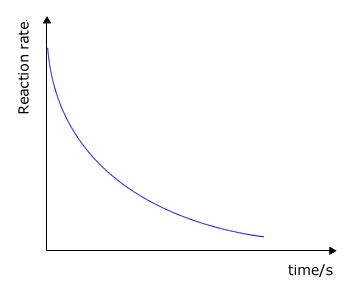
It may be clearly seen that there is some unspecified relationship between the rate of a chemical reaction and the concentration of the reactants. As a reaction progresses the concentrations of the reactants decreases and so does the rate. Look at the typical graphs below:
 |
 |
|
reactant concentration against
time
|
reaction rate against time
|
The question is, exactly what is the relationship between a specific reactant concentration and the rate? This relationship can only be established by actually performing experiments to obtain data about the rate of the reaction when the concentrations of the reactants are changed (at constant temperature).
General relationships between variables
All relationships between two variables can be represented by an equation. This would be the equation for the graph obtained showing how the two factors vary with one another.
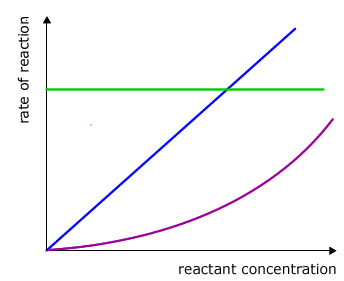
There are only three logical possibilities for a relationship between two variables, for example A and B.
- 1 No relationship at all - Change in A does not affect B
- 2 A directly proportional relationship - Change in A causes a corresponding change in B
- 3 A relationship that is not directly proportional - Change in A causes a non-linear change in B
 |
|
dependency of rate on concentration
|
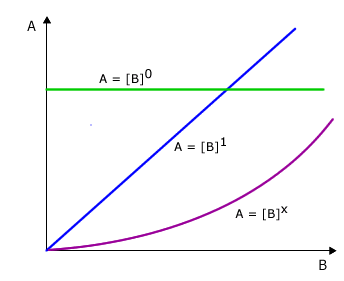
All of these possible relationships can be covered by the simple mathematical formula A = Bx
Possibility 1: No relationship at all
In this case the value of x is zero and the equation becomes A = B0
Any number raised to the power of zero = 1 so the equation reduces to A = 1, in other words there is no change in the value of B when A changes.
Possibility 2: Direct proportionality
In this case the value of x = 1 and the equation reduces to A = B1
Any number raised to the power of 1 is that number itself (eg: 21 = 2, 31 = 3, etc). In other words when A changes this causes a change by exactly the same factor in B. For example, if the value of A doubles then the value of B must double also.
Possibility 3: Some other relationship
In this case the value for x is some other number apart from 0 or 1. The value of x depends on the manner in which B changes with change in A. For the time being let's leave it as the unknown value 'x'.
 |
|
Possible relationships between
A and B
|
The rate expression
Having established that the relationship between rate and concentration can be expressed mathematically, let's consider a reaction in which two hypothetical reactants A and B react together to produce a product 'C'.
| A + B |
The rate of the reaction is dependent on (proportional to) the concentration of A (expressed using square brackets [A]) raised to some unknown power 'x', but it is also dependent on reactant B concentration, [B] raise to a different power 'y'
Therefore:
| Reaction rate = constant1 x [A]x and Reaction rate = constant2 x [B]y |
Combining these equations this becomes:
| Reaction rate = constant (combined from constants 1 and 2) x [A]x x [B]y |
This is known as the rate equation:
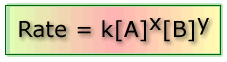
Where: k is the rate constant, x and y are the orders of the reaction with respect to the concentrations of A and B respectively.
Solving the rate equation
The rate equation can only be solved through experiment. For a two component reaction, A + B, the procedure is as follows:
1. A series of experiments are performed, keeping the reactant concentration, A, constant, but changing the concentration of B. The value of [A]x must therefore be constant throughout the experiments and can be combined with the rate constant, k to give the equation:
| Rate = constant x [B]y |
1. The effect of the change in concentration of B can now be seen on the rate. For example, if the concentration of B is doubled and the rate also doubles, then this means that the value of y = 1; If there is no effect on the rate when [B] is changed, then y = 0; if the rate increases by a factor of 4 when the concentration of B doubles, then the value of y = 1.
3. More experiments are now carried out keeping [B] constant while varying [A]. The value of [B]y is now constant and the rate equation becomes:
| Rate = constant x [A]x |
4. The effect of the change in concentration of A can now be seen on the rate. For example, if the concentration of A is doubled and the rate also doubles, then this means that the value of x = 1; If there is no effect on the rate when [A] is changed, then x = 0; if the rate increases by a factor of 4 when the concentration of A doubles, then the value of x = 1.
5. Now that values for x and y, the orders of the reaction, have been found, they can be used in any of the experiments to find the value of k, the rate constant, from any of the experimental data.
| Rate = k [A]x[B]y |
|
Example: For the reaction, X(g) + Y(g)
Calculate the initial rate of the reaction in Exp. 4. Inspection of Experiments 1 and 2 show that the concentration of Y remains constant therefore any effect on the rate is due to change in [X]. BUT as can be seen, when [X] doubles the rate stays the same. This means that change in [X] has no effect on the rate. Therefore:
Inspection of Experiments 1 and 3 show that the concentration of X remains constant therefore any effect on the rate is due to change in [Y]. AND as can be seen, when [Y] doubles the rate also doubles. This means that change in [Y] causes the same change in the rate. Therefore:
Combining these two equations gives:
As [X] does not affect the rate, we need only look at the change in [Y]. From experiments 3 to 4, [Y] doubles therefore the rate should double as well. Therefore new rate in experiment 4 = 1.48 x 10-2 mol/min |

