|
No gases meet ideal conditions one hundred percent, but most gases behave in such a way as to approximate to this 'ideal' situation. Gases theoretically behaving in this way are said to be "Ideal gases". Syllabus referenceStructure 1.5.2 - Real gases deviate from the ideal gas model, particularly at low temperature and high pressure.
Guidance
Tools and links
|
Real gases
Real gases deviate from ideal behaviour but only by small amounts under low pressures.
Deviation from ideal behaviour at high pressure
At high pressures, distances between gas particles are fairly small, and attractive forces between them becomes significant. Neighboring molecules exert an attractive force, which reduces the interaction of molecules with the container walls. The apparent pressure will be less than ideal (PV/RT will consequently be less than ideal).
As pressures increase, the volume of the gas molecules themselves becomes significant in relationship to the container volume and PV/RT will be higher than ideal (V is higher).
Ideal behaviour at high temperature
At high temperatures, the kinetic energy of the molecules is much more important
than the forces of attraction and the gases behave more ideally
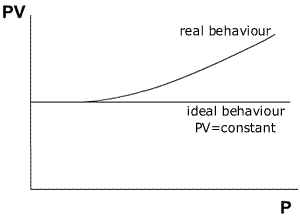The
relationship between pressure and ideality may be shown by a graph of PV against
Pressure (at constant temperature).
The graph shows that an ideal gas maintains the value of PV=constant over a very large range of different pressures. A non-ideal gas (real gas) shows a deviation from the relationship PV= constant as the pressure increases to high levels.
The curve obtained from real gases differs according to the gas used. Fortunately, experiments at pressures normally used in the laboratory give good agreement between the gas laws and the observed behaviour.
Ideal gas equation correction
Experimentation on the pressure and volume characteristics of real gases was carried out by Van der Waal, but will not be required of IB students.
Following the results of his experiments, Van der Waal introduced some modifications to the ideal gas law to compensate for the actual volume occupied by the particles themselves and the forces that exist between the particles. As stated above, the pressure of real gases is reduced by attractions between particles, and the available volume for movement is reduced due to the volume occupied by the particles themselves.
The ideal gas equation, PV = nRT becomes:
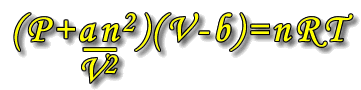
Where a and b are constants that are unique to each type of gas.
