|
The Arrhenius equation relates the rate constant, k to the activation energy of a reaction, Ea. It affords a means of determining activation energies by experimentally finding the rate constant at different temperatures |
The Arrhenius equation
The actual dependence of the rate constant on temperature is given by the Arrhenius equation.
|
k = Ae-Ea/RT
|
Where:
- k is the rate constant
- A is the Arrhenius factor (different for every reaction)
- e is the natural log base
- Ea is the minimum energy required for a reaction to take place (known as the activation energy)
- R is the universal gas constant (8.314 J kg-1 ºC-1)
- T is the absolute temperature in Kelvin
Arrhenius' constant, A - the pre-exponential factor
It is possible for colliding particles to possess enough energy for reaction, but still not have a successful collision (one that results in reaction). This is accounted for by the Arrhenius constant 'A' , also called the pre-exponential or frequency factor.
Imagine a collision between two cars; clearly more damage is going to be caused by a head on collision than a glancing scrape.
The Arrhenius constant (pre-exponential or frequency factor) is a number between 0 and 1, that reflects the proportion of successful collisions amongst those particles with enough energy for reaction.
For example, when A is very small, only a small proportion of collisions lead to reaction, regardless of the energy. When A = 1, all collisions with sufficient energy cause reaction.
Using the Arrhenius equation
In reality, the basic form of the Arrhenius equation is not very convenient for graphing or analysing date. To analyse experiments at different temperatures we usually use the natural log form of the equation:
k = Ae-Ea/RT
taking natural logs throughout this gives:
lnk = lnA - Ea/RT
Thus a plot of lnk against 1/RT, 1/T or any variation, will allow us to find the activation energy of a specific reaction as a function of the gradient, and the Arrhenius constant as a function of the intercept to the y axis.
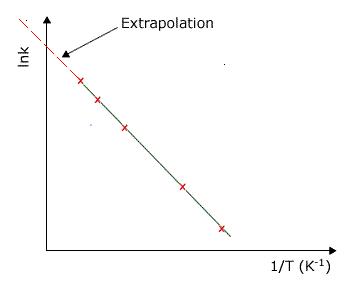 |
A typical plot used to calculate the activation energy from the Arrhenius equation. In this graph the gradient of the line is equal to -Ea/R Extrapolation of the line to the y axis gives an intercept value of lnA When the temperature is increased the term Ea/RT gets smaller. This means in turn, that the term e-Ea/RT gets bigger. |
Alternatively two results may be analysed simultaneously to obtain values for Ea, the activation energy and the Orientation factor, A. This is not particularly reliable as only two values for the rate constant are used at two different temperatures. This can introduce large errors because of too little data.
|
Example: Calculate the rate constant when T = 300K (A = 0.3, Ea = 50kJ mol-1) k = Ae-Ea/RT Ea/RT = 50000/(8.314 x 300) = 20.05 e-Ea/RT = 1.97 x 10-9 k = Ae-Ea/RT k = 5.90 x 10-10 |
|
Example: The rate of a reaction A(g) + B(g) → C(g) + D(g) has been studied as a function of temperature between 5000 and 18000 K. The following data were obtained for the rate constant:
Calculate the activation energy for the reaction. k = Ae-Ea/RT and lnk = lnA - Ea/RT from expt 1:→ ln(5.49 x 106) = lnA - Ea/ (8.314x5000) from expt 2:→ ln(9.86 x 108) = lnA - Ea/ (8.314x10000) Subtract one from the other (to remove lnA) ln(9.86 x 108) - ln(5.49 x 106) = -Ea/ (8.314x10000) + Ea/ (8.314x5000) 10000[ln(9.86 x 108) - ln(5.49 x 106)] = -Ea/8.314 + 2Ea/8.314 8.314 x 10000[ln(9.86 x 108) - ln(5.49 x 106)] = Ea 8.314 x 10000 [20.709 - 15.518] = Ea 8.314 x 10000 x 5.191 = Ea 431579.74 = Ea Ea = 432 kJ |

