Higher-level only
Certain energy changes can be measured experimentally. Combustion means 'burning'. This is one of the energy changes that lends itself to energetics studies.
Syllabus ref: R1.2.3Reactivity 1.2.3 - Standard enthalpy changes of combustion, ΔHc⦵, and formation, ΔHf⦵, data are used in thermodynamic calculations. (HL)
- Deduce equations and solutions to problems involving these terms.
Guidance
- Enthalpy of combustion and formation data aregiven in the data booklet.
Tools and links
- Structure 2.2 - Would you expect allotropes of an element, such as diamond and graphite, to have different ΔHf⦵ values?
Combustion
Combustion is the term given to burning a substance in air or oxygen. Combustion may be complete, in which case the products are completely oxidised as far as possible by the oxygen, or partial, in which case the products are not completely oxidised. Partial oxidation takes place in a limited air supply.
Complete combustion of methane
CH4 + 2O2 → CO2 + H2O
Compounds containing carbon and hydrogen, i.e. organic compounds, always produce carbon dioxide and water on complete combustion. Incomplete or partial combustion results in the formation of carbon monoxide or even carbon microparticulates.
Incomplete combustion of ethene
C2H4 + 2O2 → 2CO + 2H2O
There isn't only one equation for incomplete combustion, as there are many possible combinations of products.
The standard enthalpy of combustion
The energy released when one mole of a substance is burned in excess oxygen,
or air, under standard conditions. It is given the symbol ΔHco.
|
Example: The enthalpy of combustion of ethene may be represented by the equation: C2H4(g) + 2O2(g) → 2CO2(g) + 2H2O(l) ΔH |
REM Combustion always releases energy. It is an exothermic reaction.
Balancing energetics equations
The definition of standard enthalpy change is per mole of reactant, or product, depending on the specific energy being defined).
As energy is an extensive property, it depends on the amount of substance involved and the equations used must reflect only one mole of reactant. This can lead to fractions in the balaced equation. However, it is understood that we are dealing with energetics equations and perfectly acceptable.
Example: Show the equation that represents the standard enthalpy change of combustion of hydrogen:
Hydrogen has the formula H2, this represents 1 mole of hydrogen.
H2(g) + ½O2(g)
→ H2O(l) ΔHo = -285.8 kJ
Note that the state symbols are given for 25ºC, so that water is a liquid. State symbols must always be included in energetics equations, as there is an energy change requirement when substances move from one state to another.
Experimental determination
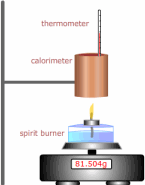
The enthalpy of combustion can be found by burning a substance under controlled conditions and using the energy released to heat a known mass of water.
There are much more accurate methods involving calorimeters (literally 'heat measurers'), which try to take into account the energy lost by radiation and other heat transfers. The data shown in books is from many experiments over the years in which the experimenters have tried to minimise the errors and now agree (within limits) to the values.
This method of enthalpy determination is riddled with errors and inaccuracies, but good enough to demonstrate the procedure.
- 1 Weigh the copper calorimeter (it's really just a copper can!) before. m1, and after filling with a quantity of water m2.
- 2 Weigh the spirit burner before the experiment. m3 - this time in grams
- 3 Record the temperature of the water in the can (calorimeter).
- 4 Light the spirit burner and allow the temperature to rise by at least 20ºC stirring gently to mix thoroughly.
- 5 Weigh the spirit burner after the experiment in grams again. m4.
Mass of the water = m2 - m1 kg
The energy change in the water = Mass (kg) x specific heat capacity of water x temperature rise (ºC)
energy change = mcΔT
This gives the energy change for the mass of liquid burned.
To calculate the energy change per mole:
Mass of liquid burned = m4 - m3 g
Moles = mass of liquid burned/ relative molecular mass of the liquid
Energy change per mole = energy calculated above/number of moles burned
ΔHc = Energy change per mole
Errors and inaccuracies
The major error in this setup is heat loss by radiation, convection and conduction. The flame only transfers a fraction of its energy to the water. Some energy is radiated away, some energy is used to heat up the can itself, some energy is used to heat up the air, some energy is used to heat up the thermometer etc.
Possible improvements
There are several ways that the experiment can be improved.
- Perform the experiment using an inflammable liquid with a known enthalpy of combustion and work out the percentage efficiency of the apparatus. Use this value to compensate for losses in other experiments.
- Try to find the specific heat capacity of the copper can and use its mass to calculate the energy loss in heating it up.
- Shield the apparatus from draughts.
- Plot a cooling curve of water in the can to find heat loss from the water by radiation.
The bomb calorimeter
The bomb calorimeter (not included in the Syllabus requirement) is a means of more accurately measuring enthalpies of combustion. It is recommended to understand the principles involved, to further the appreciation and understanding of the errors inherent in simple laboratory experiments.
Basically, the apparatus consists of a sealed chamber into which a known mass of an inflammable substance is introduced, along with excess oxygen. The heat capacity of the whole apparatus is known, to take into account in the calculations.
The explosive mixture is ignited by a small spark applied electronically using a known amount of electrical energy. The mixture burns rapidly and all of the heat energy released increases the temperature of the apparatus.
The energy released is calculated using:
E = (heat capacity of the calorimeter x ΔT)
The Standard combustion enthalpy is then calculated from:
ΔHo
= E/moles
Enthalpy of combustion data
Combustion is a process which lends itself to energetics studies and consequently most of the inflammable substances dealt with in chemistry have been determined over the years.
Researchers have investigated methods to improve the results and obtain more accurate data.
As we will see in the section on Hess' law, combustion enthalpy data may be used to calculate enthalpy data that is difficult to obtain directly through experiment, such as enthalpy of formation.
Combustion enthalpy data table
Worked examples
Q421-01 A simple calorimeter was used to determine the enthalpy of combustion of ethanol.The experimental value obtained was -920 kJ mol-1. The data booklet value is -1371 kJ mol-1. Which of the following is the best explanation for the difference between the two values?
- Incomplete combustion of the fuel
- Heat loss to the surroundings
- Poor ventilation in the laboratory
- Inaccurate temperature measurements
|
In virtually 100% of energetics experiments the major error is heat loss to the surroundings. |
Q421-02 The standard enthalpy of combustion H
| Alkanol | CH3OH methanol |
CH3CH2OH ethanol |
CH3CH2CH2OH propan-1-ol |
CH3CH2CH2CH2OH butan-1-ol |
| H |
-715 | -1371 | -2010 | -2673 |
| Mr | 32.0 | 46.0 | 60.0 | 74.0 |
Use the data to calculate the relative molecular mass of pentan-1-ol and
estimate Hoc
for pentanol.
|
As the relative molecular mass increases in regular steps of 14 units, corresponding to CH2 groups, the enthalpy of combustion also increases in a regular manner. The increase between methanol and ethanol is 656 kJ, the increase from ethanol to propan-1-ol is 639 kJ, the increase from propan-1-ol to butan-1-ol is 663 kJ. A reasonable estimate for the next member in the series would be -2673 - 650 = -3323 kJ. Another method of estimating the value of pentan-1-ol is to graph the enthalpy against the relative molecular mass and extrapolate the line of best fit to RMM = 88. |
Q421-03 What is the equation for the complete combustion of ethene?
Answer
|
Q421-04 Expressing the number of carbon atoms as 'n', what is the general equation for complete combustion of an alkane.
Answer
|
The general formala for an alkane is CnH(2n+2). All of the carbon turns into carbon dioxide = nCO2, and all of the oxygen turns to water = (2n+2)/2 H2O Thus the total moles of oxygen = n + (2n+2)/4 O2 = (6n +2)/4 = (3n + 1)/2 Hence the overall equation:
|
Q421-05 If the standard enthalpy of combustion of methanol is -715 kJ, calculate the energy released by 1 kg of methanol when burned.
Answer
|
1 kg of methanol = 1000/32 mol = 31.25 mol 1 mol releases 715 kJ therefore 31.25 mol releases 715 x 31.25 = 22343 kJ |
Q421-06 The standard enthalpy of combustion of butane is -2877 kJ. Calculate the mass of butane needed to produce 100,000 kJ of energy.
Answer
|
100,000 kJ of energy can be produced by 100,000/2877 moles = 34.76 mol 1 mol of butane = 58 g Therefore 34.76 moles = 2016 g = 2.016 kg |
Q421-07 Calculate the mass of hydrogen needed to heat 1kg of water by 10ºC. The standard enthalpy of combustion of hydrogen = -285.8 kJ, specific heat capacity of water = 4.18 kJ kg-1 ºC-1.
Answer
|
Energy needed to heat up 1 kg of water by 10ºC = 1 x 4.18 x 10 = 41.8 kJ 1 mole of hydrogen can provide 285.8 kJ therefore moles of hydrogen needed = 41.8/285.8 = 0.146 moles Mass of hydrogen gas needed = 0.146 x 2 = 0.293 g |
Q421-08 Petrol is mainly 2,2,4-trimethyl pentane, C8H18, standard enthalpy of combustion = -5461 kJ. Calculate the energy released by complete combustion of 1 dm3 of petrol. Take the density of petrol to be 0.737 kg dm-3.
Answer
| Density of petrol = 0.737 kg dm-3
Hence 1 dm-3 has a mass of 0.737 kg Relative mass of 2,2,4-trimethyl pentane, C8H18, = 114, therefore 0.737 kg = 737/114 moles = 6.465 moles. 1 mole produces 5461 kJ of energy on combustion therefore 6.465 moles produces 6.465 x 5461 kJ = 35305 kJ |
Q421-09 The density of liquid hydrogen is 67.76 g dm-3. Calculate the energy that is released on combustion of 1 dm3 of liquid hydrogen. [standard enthalpy of combustion of hydrogen = -285.8 kJ, ignore enthalpy of vaporisation.]
Answer
|
Mass of 1 dm-3 of hydrogen = 67.76 g = 67.76/2 moles = 33.88 moles. 1 mole produces 285.8 kJ of energy on complete combustion therefore 33.88 moles produces 33.88 x 285.8 = 9683 kJ |
Q421-10 The standard enthalpy change for the combustion of phenol is -3050 kJ mol-1 at 298K. Write an equation for the complete combustion of phenol, C6H5OH(s).
Answer
|
| Now test yourself |