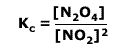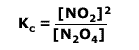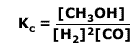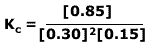IB Colourful Solutions in Chemistry

The equilibrium law is a mathematical treatment of the ratio of product and reactant concentrations under equilibrium conditions. It is also called the law of mass action.

Syllabus reference R2.3.6

Reactivity 2.3.6 - The equilibrium law is the basis for quantifying the composition of an equilibrium mixture. (HL)

Solve problems involving values of K and initial and equilibrium concentrations of the components of an equilibrium mixture.

Guidance

The approximation [reactant]initial ≈ [reactant]eqm when K is very small should be understood.
The use of quadratic equations is not expected.
Only homogeneous equilibria will be assessed.

Tools and links

Reactivity 3.1 - How does the equilibrium law help us to determine the pH of a weak acid, weak base or a buffer solution?

Equilibrium calculations
Use of approximation
Worked examples
Now test yourself

Equilibrium calculations

All equilibrium calculations require a knowledge of the balanced equation.

Using the coefficients of the equation, the concentration of the reactants and products can be found from the equilibrium constant and vice versa.

The following methodology is used:

ICE table showing how equilbrium concentration is deduced

Equation

CH₃COOH

C₂H₅OH

→

CH₃COOC₂H₅

H₂O

Intial mol

Concentration for vol = V

1/V

Equilibrium mol if mol reacting is 'x'

1-x

Equilibrium concentration

(1-x)/V

x/V

The balanced equation tells us the relationship between the moles of reactants and the moles of products. In the equation above 1 mole of each reactant produces 1 mole of each product. 1 mole of each reactant has been chosen purely for convenience. Any other quantity could have been used in the example.

The equilibrium law requires the concentrations of all of the components of the equilibrium to be known, therefore the total volume must also be known, as well as the molar amounts. In fact, if the coefficients are equal on both sides of the equation the volume terms cancel out. This is the case in the example equation, but is not always the situation.

The number of moles of product formed at equilibrium depends on the number of moles of reactants used up. The above table suggests that 'x' moles of reactants are used up from an initial number of 1. This leaves (1-x) moles of each reactant. Again, this relationship depends on the coefficients of the equation. If two moles of a product are formed from one mole of a reactant, then if x moles react there will be (1-x) moles of reactant remaining, whereas there is 2x moles of product at equilibrium.

The last step is to convert the equilibrium moles of each component into concentrations using the volume.

In the above example the equilibrium law:

In this case, the volume cancels out from all of the concentrations and the equilibrium law becomes: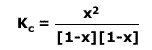

If the value of Kc is known then the value of x can be calculated using the quadratic formula. However, use of quadratic equations is not required for IB chemistry. Calculations may be required when 'x' is given in the question.

Example: When 1.0 mole of ethanoic acid is mixed with 1.0 mole of ethanol and the mixture allowed to reach equilibrium the following reaction occurs:

CH₃COOH(l) + C₂H₅OH ⇋ CH₃COOC₂H₅(l) + H₂O(l)

If the amount of ethyl ethanoate and water at equilibrium are both 0.67 moles, calculate the value of the equilibrium constant, Kc.

^ top

Use of approximation

In the equilibrium law equation various simplications may be applied by the use of approximations that do not affect the final answer, but which do make the calculations much easier.

If the value of the equilibrium constant is very small (less than 1), this means that very little of the reactants are used up in the equilibrium reaction. We can approximation the equilibrium concentration of the reactants to the initial concentration, without affecting the final answer to any significant amount.

Example: In an experiment to investigate the equilibrium:

N₂(g) + O₂(g) ⇋ 2NO(g)

the initial concentrations are N₂(g) = 1.6 mol dm^-3 and O₂(g) = 1.6 mol dm^-3. Calculate the concentration of the NO (g) after equilibrium has been established. (Kc = 1.7 x 10^-3)

In this case the equilibrium constant is very small, so we can assume that the equilibrium concentration of the reactants is the same as the initial concentration.

Equation

N₂(g)

O₂(g)

⇋

2NO(g)

Initial concentration, mol/litre

1.6

Equilibrium concentration

1.6

Here we have assumed that 'x' moles of reactants have reacted and hence formed 2x moles of product. As we are given concentrations not moles, we can assume that the volume is 1 dm³ for convenience.

By the equilibrium law:

Filling in the values: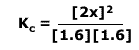

Rearranging and substituting for Kc: 4x² = 2.56 x 1.7 x 10^-3

Therefore x = √1.09 x 10^-2

Therefore x = 0.104

The final concentration of NO is 2x = 0.208 mol dm^-3

Equilibrium law quick check

^ top

Worked examples

Q236-01 The equilibrium between nitrogen dioxide (dark brown) and dinitrogen tetroxide (colourless) is represented by the reaction:

2NO₂(g) ⇋ N₂O₄(g) ΔH = -57.2 kJ mol^-1; Kc = 1 at 328K

If 4 moles of N₂O₄(g) are present in a 1dm³ flask at equilibrium, calculate the concentration of the NO₂(g).

Answer

Equation:	2NO₂(g)	N₂O₄(g)
Initial concentration/ mol dm^-3	?	?
Equilibrium concentration	?	2

By the equilibrium law:

Therefore: 1 = 4/[NO₂]²

Therefore: [NO₂]² = 4

Therefore [NO₂] at equilibrium = 2 mol dm^-3

Q236-02 When 1 mole of hydrogen iodide is allowed to dissociate into its elements at 440ºC in a 1dm³ vessel, only 0.78 moles of hydrogen iodide are present at equilibrium. Calculate the value of the equilibrium constant at this temperature.
Answer

The equation for the equilibrium reaction is:

2HI(g) ⇋ H₂(g) + I₂(g)

Using the equilibrium table:

Equation:	2HI(g)	H₂(g)	+	I₂(g)
Initial concentration/ mol dm^-3	1	-		-
Equilibrium concentration	0.78	0.11		0.11

From stoichiometry of the equation, when 0.22 moles of HI reacts it makes half as many moles of hydrogen and iodine, i.e. 0.11 moles.

The values can now be substituted into the correct equilibrium law expression:

Therefore Kc = (0.11 x 0.11)/0.78²

Therefore Kc = 0.0199 (three sig figs)

Q236-03 The expression for the equilibrium constant for a reaction is:

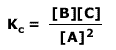
At a certain temperature the values of [A], [B] and [C] are all 0.2 mol dm^-3. What happens to the value of Kc when all three values are doubled to 0.4 mol dm^-3?

Answer

Substitute for [A], [B] and [C] to find Kc for the first condition:

Kc = 0.04/0.04 = 1

After changing the concentrations

Kc = 0.16/0.16 = 1

There is no change in the value of Kc

Q236-04 In the equilibrium:

N₂O₄(g) ⇋ 2NO₂(g)

The 1 mol of N₂O₄(g) in a 1dm³ flask at 25ºC became 0.8 mol of N₂O₄(g) when equilibrium had been established.

Calculate: The number of moles of NO₂(g) present at equilibrium and the numerical value of Kc with units.

Answer

Using the equilibrium table method:

Equation:	N₂O₄(g)	2NO₂(g)
Initial concentration/ mol dm^-3	1	-
Equilibrium concentration	(1-x) = 0.8	2x

From the moles used up ('x') we can see that 2x moles are formed = 2 x 0.2 = 0.4 moles of NO₂(g)

Using the equilibrium law expression:

Therefore Kc = (0.4)²/0.8 = 0.2 mol dm^-3

Q236-5 Methanol is an important industrial solvent and fuel. It can be produced from carbon monoxide and hydrogen according to the equation:

CO(g) + 2H₂(g) ⇋ CH₃OH(g) ΔH = -91 kJmol^-1

Calculate a value for the equilibrium constant, Kc, if the maximum yield of methanol is 85%.

Answer

If the maximum yield of methanol is 85%, this means that 85% of the reactants in an ideal mixture react completely. If we let the volume of the container be equal to 1dm³ and the initial moles of CO = 1 mol and H₂ = 2 mol, then:

Equation:	CO(g)	+	2H₂(g)	CH₃OH(g)
Initial concentration/ mol dm^-3	1		2	0
Equilibrium concentration	0.15		0.30	0.85

Using the equilibrium law expression:

Therefore:

Therefore at equilibrium Kc = 63.0 (3 significant figures)

Now test yourself

^ top