Standard level
As discussed in section 3.11, matter is built up with one of five structures. This section deals with the approach used when discussion the particles involved in matter according to its structure
Syllabus ref: S1.4.4Structure 1.4.4 - The empirical formula of a compound gives the simplest ratio of atoms of each element present in that compound. The molecular formula gives the actual number of atoms of each element present in a molecule.
- Interconvert the percentage composition by mass and the empirical formula.
- Determine the molecular formula of a compound from its empirical formula and molar mass.
Guidance
Tools and links
- Tool 1 - How can experimental data on mass changes in combustion reactions be used to derive empirical formulas?
- Nature of science, Tool 3, Structure 3.2 - What is the importance of approximation in the determination of an empirical formula?
Percentages in maths
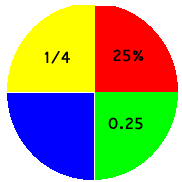
The term "percentage" means parts in every hundred. Simple fractions may be scaled up to be out of one hundred when the numerator (the number on the top) becomes the percentage.
One quarter is written 1/4 or, out of one hundred, this becomes 25/100 = 25%
It is useful to become familiar with the relationship between simple fractions, decimals and percentages.
| fraction | decimal | percentage |
|---|---|---|
|
1/2
|
0.50
|
50%
|
|
1/3
|
0.33
|
33%
|
|
2/3
|
0.67
|
67%
|
|
1/4
|
0.25
|
25%
|
|
3/4
|
0.75
|
75%
|
|
1/5
|
0.20
|
20%
|
|
2/5
|
0.40
|
40%
|
|
3/5
|
0.60
|
60%
|
|
4/5
|
0.80
|
80%
|
|
1/8
|
0.125
|
12.5%
|
Percentage composition
The percentage composition of a material is generally taken to mean the percentage by mass of the elements within a substance.
Example: Calcium carbonate - CaCO3
The relative formula mass = 40 + 12 + (3x16) = 100
Calcium makes up 40 relative mass unit parts of this formula, therefore the percentage by mass of calcium is 40/100 = 40%
Carbon makes up 12 relative mass unit parts of this formula, therefore the percentage by mass of carbon is 12/100 = 12%
Oxygen makes up 48 relative mass unit parts of this formula, therefore the percentage by mass of oxygen is 48/100 = 48%
Empirical formula
The empirical formula is the simplest ratio of atoms within a chemical compound.
From the above example it may be appreciated that the percentage by mass, when divided by the relative mass of each element, gives the relative numbers of particles in the formula.
Example: Find the empirical formula of the compound which has the following percentage by mass composition: Carbon 12.12%; Oxygen 16.16%; Chlorine 71.17%.
Divide each percentage composition by mass by the relative atomic mass.
Carbon 12.12/12 = 1.01, Oxygen 16.16/16 = 1.01, Chlorine 71.17/35.5 = 2.00
These are in the approximate integer ratio 1xC : 1xO : 2xCl
Thus the empirical formula = COCl2
This method is used to calculate the empirical formula of unknown substances. If we also know the relative formula mass, obtainable from experimental data, then the molecular formula can also be found.
Why bother with the empirical formula?
It may seem at first sight that an unusual emphasis is placed on this procedure by the various examination boards. This stems from the historic development of chemistry, from the times when determination of structure was an extremely important activity, as many new materials were being isolated and their formulae determined.
An unknown compound would be broken down into simpler substances and these measured quantitatively. By finding the percentage of the elements within the original compound it became possible to determine the empirical and, with further evidence, the molecular formula of the unknown compound.
Example: 1.6 g of an unknown organic substance X was burned in excess oxygen and the mass of carbon dioxide produced determined by absorption in concentrated KOH solution.
The mass of water was determined by first passing the gases produced from the combusion through anhydrous calcium choride.
The following results were obtained:
- Mass of carbon dioxide = 4.889g
- Mass of water obtained = 2.405g
Mass of carbon in 4.889g CO2 = 4.889 x 12/44 = 1.333g
Mass of hydrogen in 2.405g of H2O = 2.405 x 2/18 = 0.267g
percentage by mass of carbon = 1.333/1.6 = 0.833 x 100 = 83.3%
percentage by mass of hydrogen = 0.267/1.6 = 0.167 x 100 = 16.7%
empirical formula = carbon 83.3/12 : hydrogen 16.7/1
empirical formula = C 6.94 : H 16.7
This simplifies to give an empirical formula of C5H12
In summary, it is important to be able to calculate the percentage composition by mass of the elements within a compound and also to use percentage composition values to calculate the empirical formula.
Remember that the sum of all percentages by mass MUST equal 100%.
Worked examples
Q324-01 Find the molecular formula given the following percentage compositions and relative molecular mass information:Carbon = 80%, Hydrogen = 20%, Mr= 30
Answer|
Step 1. Divide the percentage composition of each element by its relative atomic mass:
Carbon = 6.67, Hydrogen = 20 Step 2. Divide each value in the ratio of the elements by the smallest value.
Carbon = 1 : Hydrogen = 3 Step 3. Make sure that all number are integers (whole numbers) by manipulation of the values (i.e. multiplying or dividing through, as appropriate) In this case they are integers already Step 4. Calculate the mass of the empirical formula obtained in step 3 and find out how many of these are needed to get the relative molecular mass. Use this number to obtain the molecular formula by multiplying it by the empirical formula. Empirical formula = CH3, relative mass = 15 Given Mr = 30 and this is equal to 15 x 2 therefore there are two empirical formula units in a molecular formula Molecular formula = (CH3) x 2 = C2H6 |
Q324-02 Find the molecular formula given the following percentage compositions and relative molecular mass information:
Carbon = 40%, Hydrogen = 6.67%, Oxygen 53.33%, Mr= 60
Answer|
Step 1. Divide the percentage composition of each element by its relative atomic mass:
Carbon = 3.33, Hydrogen = 6.67, Oxygen = 3.33 Step 2. Divide each value in the ratio of the elements by the smallest value.
Carbon = 1 : Hydrogen = 2 : Oxygen 1 Step 3. Make sure that all number are integers (whole numbers) by manipulation of the values (i.e. multiplying or dividing through, as appropriate) In this case they are already integers Step 4. Calculate the mass of the empirical formula obtained in step 3 and find out how many of these are needed to get the relative molecular mass. Use this number to obtain the molecular formula by multiplying it by the empirical formula. Empirical formula = CH2O, relative mass = 30 Given Mr = 60 and this is equal to 30 x 2 therefore there are two empirical formula units in a molecular formula Molecular formula = (CH2O) x 2 = C2H4O2 |
Q324-03 Find the molecular formula given the following percentage compositions and relative molecular mass information:
Nitrogen = 87.5%, Hydrogen = 12.5%, Mr= 32
Answer|
Step 1. Divide the percentage composition of each element by its relative atomic mass:
Nitrogen = 6.25, Hydrogen = 12.5 Step 2. Divide each value in the ratio of the elements by the smallest value.
Nitrogen = 1, Hydrogen = 2 Step 3. Make sure that all number are integers (whole numbers) by manipulation of the values (i.e. multiplying or dividing through, as appropriate) In this case they are integers already Step 4. Calculate the mass of the empirical formula obtained in step 3 and find out how many of these are needed to get the relative molecular mass. Use this number to obtain the molecular formula by multiplying it by the empirical formula. Empirical formula = NH2, relative empirical mass = 16 Given Mr = 32 and this is equal to 16 x 2 therefore there are two empirical formula units in a molecular formula Molecular formula = (NH2) x 2 = N2H4 |
Q324-04 Find the molecular formula given the following percentage compositions and relative molecular mass information:
Oxygen = 94.12%, Hydrogen = 5.88% Mr= 34
Answer|
Step 1. Divide the percentage composition of each element by its relative atomic mass:
Oxygen = 5.88, Hydrogen = 5.88 Step 2. Divide each value in the ratio of the elements by the smallest value.
Oxygen = 1, Hydrogen = 1 Step 3. Make sure that all number are integers (whole numbers) by manipulation of the values (i.e. multiplying or dividing through, as appropriate) In this case they are integers already Step 4. Calculate the mass of the empirical formula obtained in step 3 and find out how many of these are needed to get the relative molecular mass. Use this number to obtain the molecular formula by multiplying it by the empirical formula. Empirical formula = OH, relative empirical mass = 17 Given Mr = 34 and this is equal to 17 x 2 therefore there are two empirical formula units in a molecular formula Molecular formula = (OH) x 2 = H2O2 |
Q324-05 Find the molecular formula given the following percentage compositions and relative molecular mass information:
Carbon = 40%, Hydrogen = 6.67%, Oxygen 53.33%, Mr= 180
Answer|
Step 1. Divide the percentage composition of each element by its relative atomic mass:
Carbon = 3.33, Hydrogen = 6.67, Oxygen = 3.33, Step 2. Divide each value in the ratio of the elements by the smallest value.
Carbon = 1, Hydrogen = 2, Oxygen = 1, Step 3. Make sure that all number are integers (whole numbers) by manipulation of the values (i.e. multiplying or dividing through, as appropriate) In this case they are integers already Step 4. Calculate the mass of the empirical formula obtained in step 3 and find out how many of these are needed to get the relative molecular mass. Use this number to obtain the molecular formula by multiplying it by the empirical formula. Empirical formula = CH2O, relative empirical mass = 30 Given Mr = 180 and this is equal to 30 x 6, therefore there are six empirical formula units in a molecular formula Molecular formula = (CH2O) x 6 = C6H12O6 |
Q324-06 Find the molecular formula given the following percentage compositions and relative molecular mass information:
Sulfur = 23.70%, Oxygen = 23.70%, Chlorine = 52.59%, Mr= 135
Answer|
Step 1. Divide the percentage composition of each element by its relative atomic mass:
sulfur = 0.74, Oxygen = 1.48, Chlorine = 1.50 Step 2. Divide each value in the ratio of the elements by the smallest value.
sulfur = 1, Oxygen = 2, Chlorine = 1 Step 3. Make sure that all number are integers (whole numbers) by manipulation of the values (i.e. multiplying or dividing through, as appropriate) In this case they are integers already Step 4. Calculate the mass of the empirical formula obtained in step 3 and find out how many of these are needed to get the relative molecular mass. Use this number to obtain the molecular formula by multiplying it by the empirical formula. Empirical formula = SO2Cl2, relative empirical mass = 135 Given Mr = 135 and this is equal to the empirical formula mass Molecular formula = SO2Cl2 |
Q324-07 Find the molecular formula given the following percentage compositions and relative molecular mass information:
Fluorine = 95%, Hydrogen = 5%, Mr= 20
Answer|
Step 1. Divide the percentage composition of each element by its relative atomic mass:
Fluorine = 5, Hydrogen = 5 Step 2. Divide each value in the ratio of the elements by the smallest value.
Fluorine = 1, Hydrogen = 1 Step 3. Make sure that all number are integers (whole numbers) by manipulation of the values (i.e. multiplying or dividing through, as appropriate) In this case they are integers already Step 4. Calculate the mass of the empirical formula obtained in step 3 and find out how many of these are needed to get the relative molecular mass. Use this number to obtain the molecular formula by multiplying it by the empirical formula. Empirical formula = HF, relative empirical mass = 20 Given Mr = 20 and this is equal to the empirical formula mass then: Molecular formula = = HF |
Q324-08 Find the molecular formula given the following percentage compositions and relative molecular mass information:
Nitrogen = 12.28%, Hydrogen = 3.51%, sulfur 28,07%, Oxygen 56.14%, Mr= 228
Answer|
Step 1. Divide the percentage composition of each element by its relative atomic mass:
Nitrogen = 0.88, Hydrogen = 3.51, sulfur = 0.88, Oxygen = 3.51 Step 2. Divide each value in the ratio of the elements by the smallest value.
Nitrogen = 1 , Hydrogen = 4, sulfur = 1, Oxygen = 4 Step 3. Make sure that all number are integers (whole numbers) by manipulation of the values (i.e. multiplying or dividing through, as appropriate) In this case they are integers already Step 4. Calculate the mass of the empirical formula obtained in step 3 and find out how many of these are needed to get the relative molecular mass. Use this number to obtain the molecular formula by multiplying it by the empirical formula. Empirical formula = NH4SO4, relative empirical mass = 114 Given Mr = 228 and this is equal to 114 x 2 therefore there are two empirical formula units in a molecular formula Molecular formula = (NH4SO4) x 2 = N2H8S2O8 |
Q324-09 Find the molecular formula given the following percentage compositions and relative molecular mass information:
Phosphorus = 10.88%, Iodine = 89.12%, Mr= 570
Answer|
Step 1. Divide the percentage composition of each element by its relative atomic mass:
Phosphorus = 0.35, Iodine = 0.70 Step 2. Divide each value in the ratio of the elements by the smallest value.
Phosphorus = 1, Iodine = 2 Step 3. Make sure that all number are integers (whole numbers) by manipulation of the values (i.e. multiplying or dividing through, as appropriate) In this case they are integers already Step 4. Calculate the mass of the empirical formula obtained in step 3 and find out how many of these are needed to get the relative molecular mass. Use this number to obtain the molecular formula by multiplying it by the empirical formula. Empirical formula = PI2, relative empirical mass = 285 Given Mr = 570 and this is equal to 285 x 2 therefore there are two empirical formula units in a molecular formula Molecular formula = (PI2) x 2 = P2I4 |
Q324-10 Find the molecular formula given the following percentage compositions and relative molecular mass information:
Phosphorus = 43.66%, Oxygen = 56.34%, Mr= 284
Answer|
Step 1. Divide the percentage composition of each element by its relative atomic mass:
Phosphorus = 1.41, Oxgen = 3.52 Step 2. Divide each value in the ratio of the elements by the smallest value.
Phosphorus = 1, Oxygen = 2.5 Step 3. Make sure that all number are integers (whole numbers) by manipulation of the values (i.e. multiplying or dividing through, as appropriate) We have to multiply through by 2 to remove the fraction This gives Phosphorus = 2, Oxygen = 5 Step 4. Calculate the mass of the empirical formula obtained in step 3 and find out how many of these are needed to get the relative molecular mass. Use this number to obtain the molecular formula by multiplying it by the empirical formula. Empirical formula = P2O5, relative empirical mass = 142 Given Mr = 284 and this is equal to 142 x 2 therefore there are two empirical formula units in a molecular formula Molecular formula = (P2O5) x 2 = P4O10 |
Now test yourself
External video resources
Empirical and molecular formula: Richard Thornley
