Standard level
Gases, involved in chemical reactions show simple ratios between gas volumes. This makes dealing with gaseous reactions very simple in terms of calculations.
Syllabus ref: S1.5.3Structure 1.5.3 - The molar volume of an ideal gas is a constant at a specific temperature and pressure.
- Investigate the relationship between temperature, pressure and volume for a fixed mass of an ideal gas and analyse graphs relating these variables.
Guidance
- The names of specific gas laws will not be assessed.
- The value for the molar volume of an ideal gas under standard temperature and pressure (STP) is given in the data booklet.
Tools and links
- Nature of science, Tool 2 and Tool 3, Reactivity 2.2 - Graphs can be presented as sketches or as accurately plotted data points.
- What are the advantages and limitations of each representation?

Gas molar volume
Avogadro realised that if gas volumes contain the same number of particles as one another (under the same temperature and pressure conditions) then an Avogadro number of molecules of each gas will occupy the same volume. This volume is called the gas molar volume
STP, standard temperature and pressure is defined as 273K and 100 kPa pressure. Under these conditions 1 mol of an ideal gas occupies 22.7 dm3.
The "old" definition of standard pressure used 1 atmosphere, which actually equals 101.3 kPa. Under this pressure the gas molar volume is 22.4 dm3. The IUPAC has officially accepted 100kPa as atmospheric pressure, and so we must use 22.7 dm3 as the gas molar volume.
This means that the number of moles of a gas can be calculated from the volume, providing the temperature and the pressure are known.
It is important to be consistent with the volume units used. In the equation triangle above, the units are litres for all volume measurements.
Example: Calculate the number of moles of present in 10 dm3 of gas at STP
1 mole of gas occupies 22.7 dm3 at STP
therefore moles of gas = volume (in litres) /22.7
Moles of gas = 10/22.7
Moles of gas = 0.441 moles
If the conditions are not STP (standard temperature and pressure) then the ideal gas equation PV = nRT must be used to find the number of moles.
Boyle's law
Robert Boyle found that for a given number of moles of gas the volume of the gas is proportional to its pressure provided the temperature is kept constant.
This can be expressed as:
The pressure of a gas derived from collisions of the gas particles with the walls of the container. If the volume is decreased then the gas particles are resticted to less space and there are more collisions per second at the walls and consequently a greater pressure is exerted.
Boyles law allows calculation of new volume and/or pressure conditions (at constant temperature) in, for example, a piston or gas syringe.
Example: Calculate the pressure when 100cm3 of gas at atmospheric pressure is compressed to 10cm3 at constant temperature.
Boyle's law states that PV is constant therefore the initial product of the pressure times the volume must equal the final product of the pressure times the volume, i.e.:
P1V1 = P2V2
P1 = 1.01 x 105 Pa, V1 = 0.1dm3, V2 = 0.01dm3, P2 = ?
P2 = (1.01 x 105 x 0.1)/0.01
P2 = 1.01 x 106 Pa
Charles' law
He found that for a given number of moles of gas the volume of the gas is inversely proportional to its temperature, provided the pressure is kept constant.
This may be expressed as:
This relationship can be explained by considering the effect that temperature has on the average kinetic energy of the gas particles. Increase the temperature and the particles increase in energy and speed. Collisions between particles force the gas apart and if the pressure is kept constant then the gas expands.
Charles' Law is useful for calculating the change in a gas volume under different temperature conditions. Gases are not usually dealt with under standard conditions and so this law allows correction for the current temperature.
Note: the temperature referred to is ALWAYS the absolute temperature in Kelvin, where 0 Kelvin = -273ºC.
Forgetting to change the temperature data into kelvin is a common mistake in calculations involving the gas laws.
Example: Calculate the volume occupied by 1 mole of gas at 35ºC at atmospheric pressure.
At STP (273K, 1 atmosphere pressure) 1 mole of any gas occupies 22.7 dm3
According to Charles' Law:
|
V1
|
=
|
V2
|
|
T1
|
T2
|
|
V1T2
|
=
|
V2
|
|
T1
|
|
22.7 x 308
|
=
|
V2
|
|
273
|
New volume = 25.6 dm3 (3 sig. figs)
The equation of state
The equations of Boyle's law (PV = constant) and Charles' law (V/T = constant) may be combined to give the expression: PV/T = constant. This is called the equation of state. This new combined gas equation can be used to find the new volume, pressure and temperature of a gas if the conditions are changed.
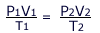


External video resources
Analysing graphs related to the ideal gas law: Richard Thornley